Question

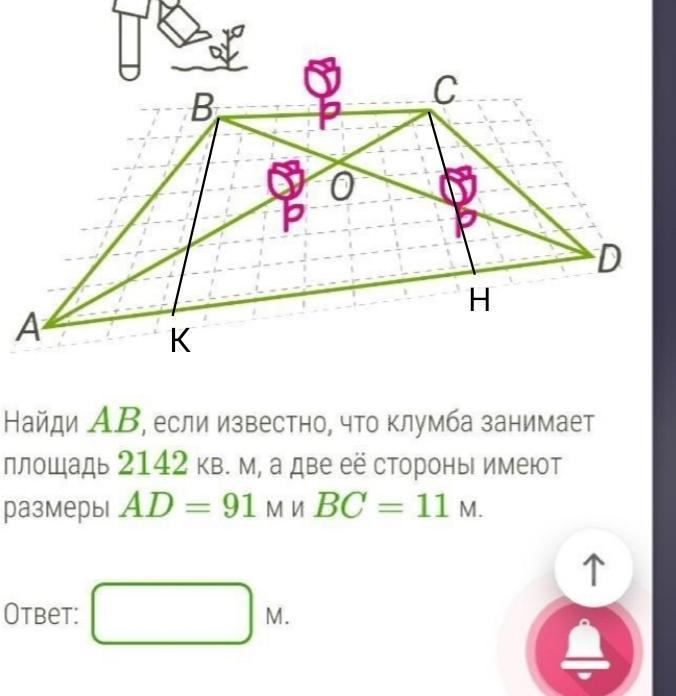
В парке при музее решили разбить клумбу в форме четырёхугольника. Две стороны этой клумбы (AD и BC), если бы можно было продлить их на бесконечную длину, никогда б не пересеклись. Другие две (AB и CD), если бы можно было продлить их на бесконечную длину, сошлись бы когда-нибудь одной точке. Оба тупых угла, образованных смежными сторонами этого четырёхугольника, оказались равны.     Найди AB, если известно, что клумба занимает площадь 2142 кв. м, а две её стороны имеют размеры AD=91 м и BC=11 м.   помогиттеееее
​

Answer 1

Ответ:

АВ=58м

Объяснение:

S=BK(BC+AD)/2

BK=(2*S)/(BC+AD)=(2*2142)/(91+11)=

=4284/102=42м высота трапеции

АК=НD, т.к. трапеция равнобедренная.

АК=(АD-BC)/2=(91-11)/2=80/2=40м.

∆АВК- прямоугольный треугольник

По теореме Пифагора

АВ=√(АК²+ВК²)=√(40²+42²)=

=√(1600+1764)=√3364=58м