Предмет: Алгебра,
автор: Dickobraz
Докажите тождество, даю 100 баллов
Приложения:
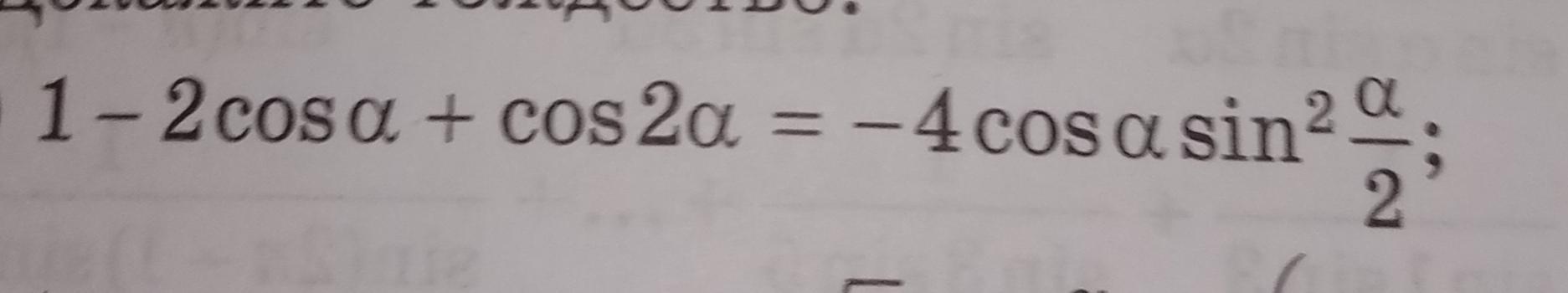
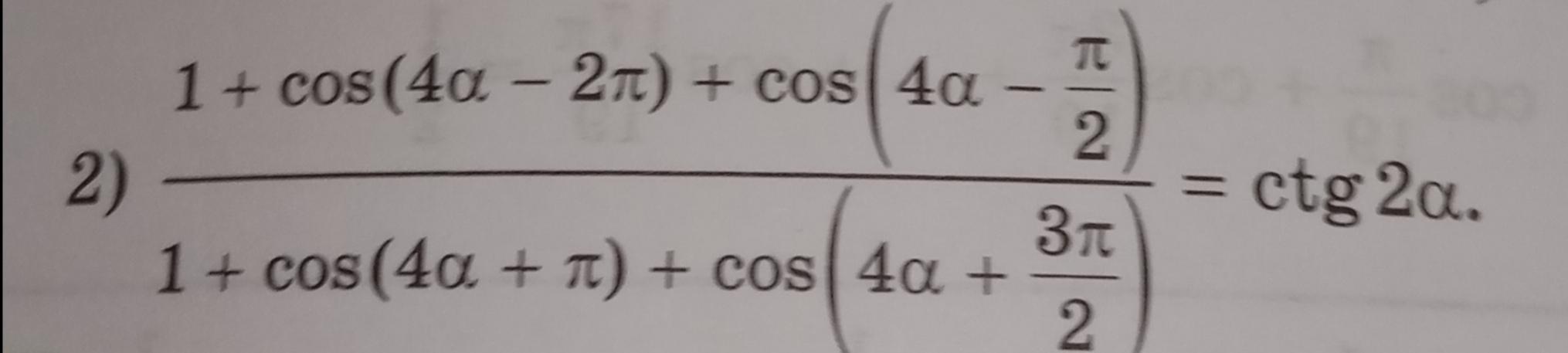
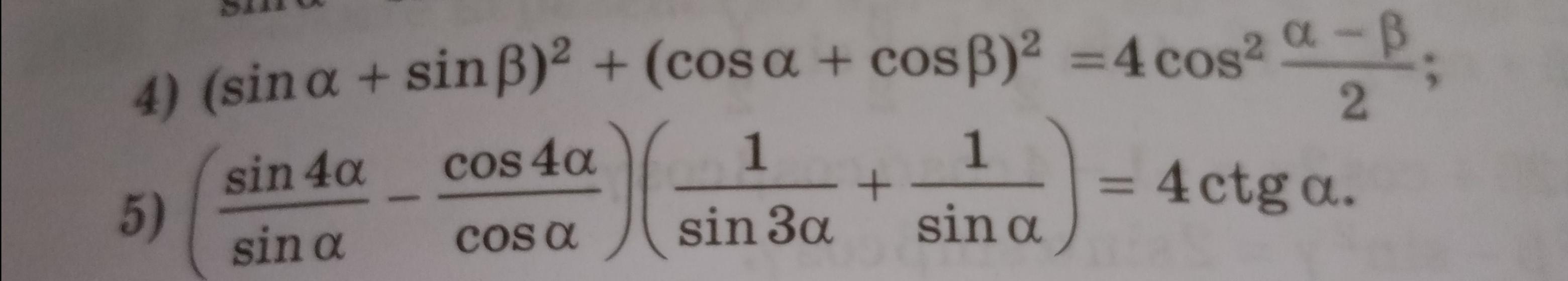
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: polina584
Предмет: Английский язык,
автор: VoolBuMarine
Предмет: Русский язык,
автор: 0014567890123
Предмет: Алгебра,
автор: ZZZZZSWISSZZZZZ