Предмет: Алгебра,
автор: Kv4zimoda
Решить уравнение, как можно подробнее
Приложения:
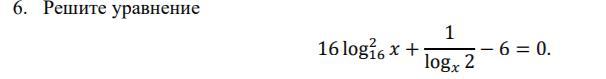
Ответы
Автор ответа:
1
ОДЗ: x>0; x≠1
Уравнение принимает вид:
D=25
или
или
или
Оба корня удовл ОДЗ
О т в е т.
Похожие вопросы
Предмет: Русский язык,
автор: Лёпачка
Предмет: Окружающий мир,
автор: ali20063
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Українська мова,
автор: маня278
Предмет: Английский язык,
автор: alusha2001