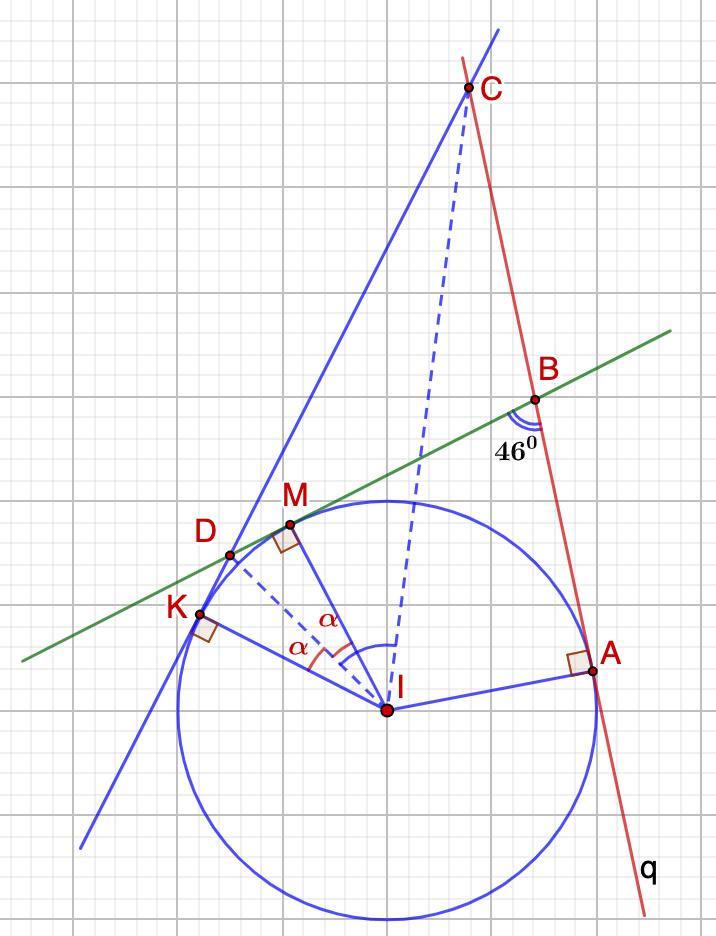
Окружность ω с центром в точке I касается прямой q в точке A. На прямой q отмечены точки B и C так, что точка B лежит между A и C. Из точек B и C к ω проведены касательные, отличные от q, которые пересекаются в точке D. Найдите величину угла CID, если угол ABD равен 46 градусам.
Ответы
Ответ:
∠DIC = 67°
Пошаговое объяснение:
Надо найти ∠CID.
Дано: ω (I; IA);
q = касательная.
B ∈ q; C ∈ q;
BM; CK - касательные;
∠ABD = 46°
Найти: ∠CID
Решение:
Для того, чтобы найти ∠CID необходимо сделать чертеж.
1. Рассмотрим ΔKDI и ΔIDM.
- Радиус, проведенный в точку касания, перпендикулярен касательной.
⇒ ΔKDI и ΔIDM - прямоугольные.
ID - общая;
- Отрезки касательных к окружности, проведённые из одной точки, равны.
⇒ DK = DM
⇒ ΔKDI = ΔIDM (по гипотенузе и катету)
⇒ ∠KID = ∠DIM (как соответственные элементы)
Пусть ∠KID = ∠DIM = α
2. ∠МВА = 46°
- Угол между двумя касательными, проведенными из одной точки, равен 180° минус градусная мера заключенной внутри него дуги, меньшей полуокружности.
⇒ ∠МВА = 180° - ∪ АМ
Подставим значение ∠МВА = 46° и найдем ∪ АМ:
46° = 180° - ∪ АМ или ∪ АМ = 180° - 46° = 134°
- Центральный угол измеряется градусной мерой дуги, на которую он опирается.
⇒ ∠MIA = ∪ AM = 134° (центральный)
3. ∠KIA = ∠MIA +2α = 134° + 2α (см. рис.) (центральный)
⇒ ∪ KMA = ∠KIA = 134° +2α
4. Рассмотрим ΔCKI и ΔICA - прямоугольные (радиус ⊥ касательной)
IC - общая;
IK = IA (радиусы одной окружности)
⇒ ΔCKI = ΔICA (по гипотенузе и катету)
∠KIC = ∠CIA (как соответственные элементы.)
5. ∠KIC = ∠CIA = ∠KIA : 2 = ( 134° +2α) : 2 = 67° + α
∠CID = ∠KIC - α = 67° + α - α = 67°
Искомый угол найден ∠CID =67°.