Question

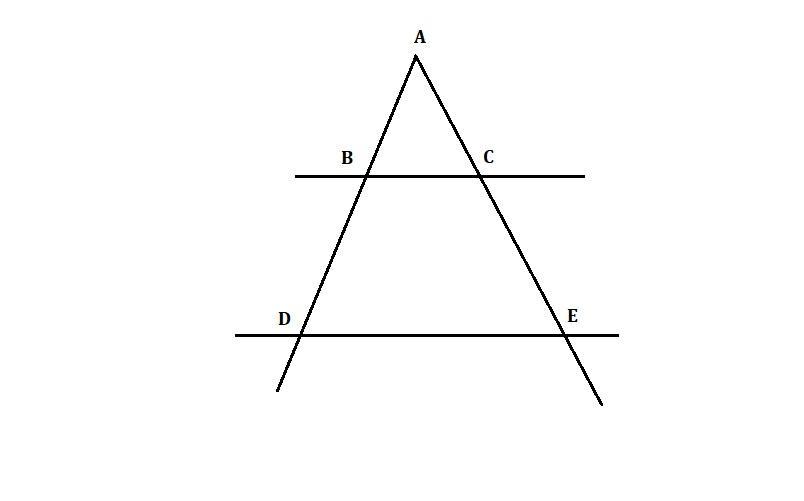
Сторони кута А перетнуті паралельними прямими BC і DE ( точки B і D розміщено на одній стороні кута а, точки C і E на іншій стороні ) . Знайти AD, одній стороні кута, а точки C і E - на іншій стороні якщо AC : AE = 15:33 і BD= 12см помогите срочно

Answer 1

Ответ:

22 cм

Объяснение:

∠АВС=∠АDE - як відповідні кути при перетині двох паралельних прямих  BC і DE та січной AD

∠ВАС=∠DАE - як спільний

⇒ΔАВС ~ ΔАDE за двома кутами

• Якщо два кути одного трикутника відповідно дорівнюють двом кутам іншого, то такі трикутники подібні. (Перша ознака подібності трикутників)

З подібності трикутників випливає пропорційність відповідних відрізків :

$\dfrac{AB}{AD} =\dfrac{AC}{AE} \\\\\dfrac{AB}{AD} =\dfrac{15}{33} \\\\33AB=15(AB+12)\\\\33AB=15AB+180\\\\18AB=180\\\\AB=10$

АВ = 10см, AD = АВ+BD=10+12=22см