Предмет: Алгебра,
автор: irinasaz080
Помогите!Тут вроде все просто....
Приложения:
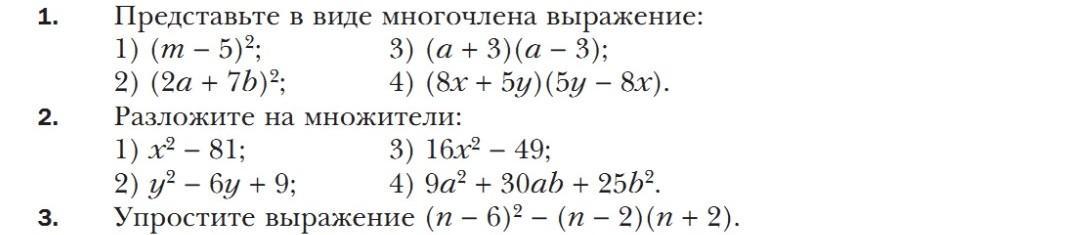
Аноним:
так решай сам, если тут все просто!
Ответы
Автор ответа:
4
Для решения этих задач нам понадобится несколько формул (нумерация свободная для более краткого пояснения - перед каждым решением я указала порядковый номер формулы, чтобы было понятно, откуда что берется).
1) - квадрат суммы
2) - квадрат разности
3) - разность квадратов
Задание 1.
а) 2 формула.
б) 1 формула.
в) 3 формула.
г) 3 формула + перестановка слагаемых в первой скобке (от перестановки мест слагаемых сумма не меняется).
Задание 2.
1) 3 формула.
2) 2 формула.
3) 3 формула.
4) 1 формула.
Задание 3.
Первую скобку раскрываем по 2 формуле, вычитаемое же представляет собой разность квадратов (3 формула).
можешь также решить 1 вариант?
Похожие вопросы
Предмет: Русский язык,
автор: gov2006Lisënok
Предмет: Английский язык,
автор: Тигр1111111
Предмет: Русский язык,
автор: Ванлавчица
Предмет: Геометрия,
автор: Akonakote