Предмет: Алгебра,
автор: cem3112005
Помогите пожалуйста упростить выражения
Приложения:
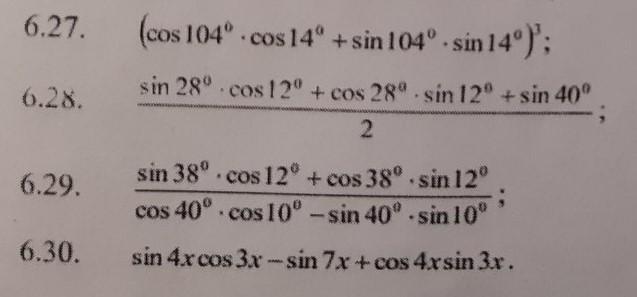
Ответы
Автор ответа:
1
Відповідь:
Пояснення:
тримай
Приложения:

Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: TheDarkusAkwio
Предмет: Русский язык,
автор: Amallol
Предмет: Русский язык,
автор: Зайка26516736742
Предмет: Қазақ тiлi,
автор: aida5256
Предмет: Русский язык,
автор: Roman7000000