Предмет: Алгебра,
автор: ozodayusupova168
Помогите пожалуйста только с номером 343. Нужно очень срочно !
Приложения:
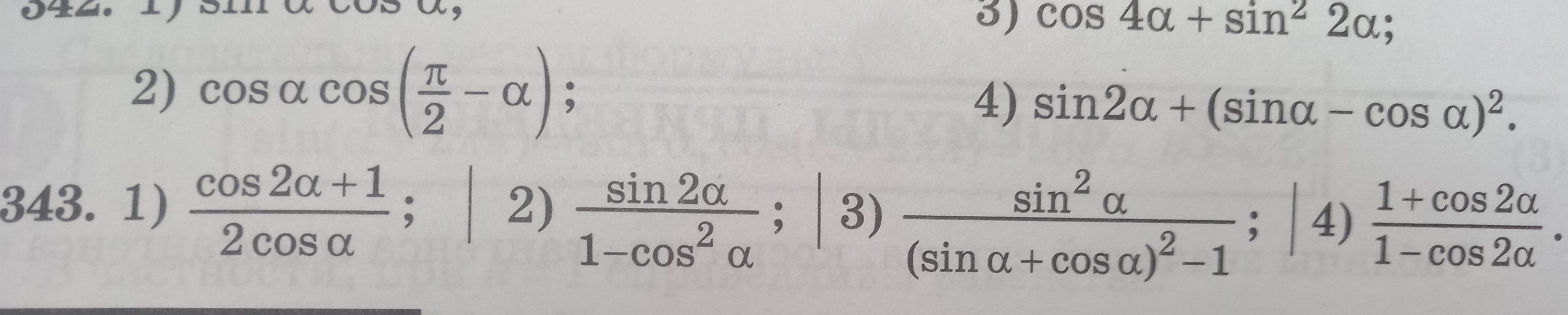
XNyuton:
решение обязательно?
Дааа ооочень нужно
Ответы
Автор ответа:
1
Объяснение:
1) Воспользуемся формулой
2) Воспользуемся формулами
3) Воспользуемся формулами
4) Воспользуемся формулой
Похожие вопросы
Предмет: Русский язык,
автор: isazonov2004
Предмет: Русский язык,
автор: Pichkurenko80
Предмет: Английский язык,
автор: elsiyarislyamo
Предмет: Математика,
автор: dimas560
Предмет: Алгебра,
автор: kira74969