Предмет: Алгебра,
автор: masha01021
Помогите пожалуйста, решить, производная
Приложения:
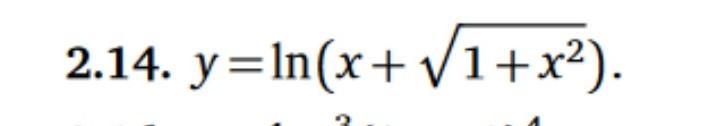
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: СеКРеТатьяны
Предмет: Русский язык,
автор: лора63
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: Снежа18012004
Предмет: ОБЖ,
автор: artyom121961