Question

Помогите пожалуйста решить две задачи, всё подробно только

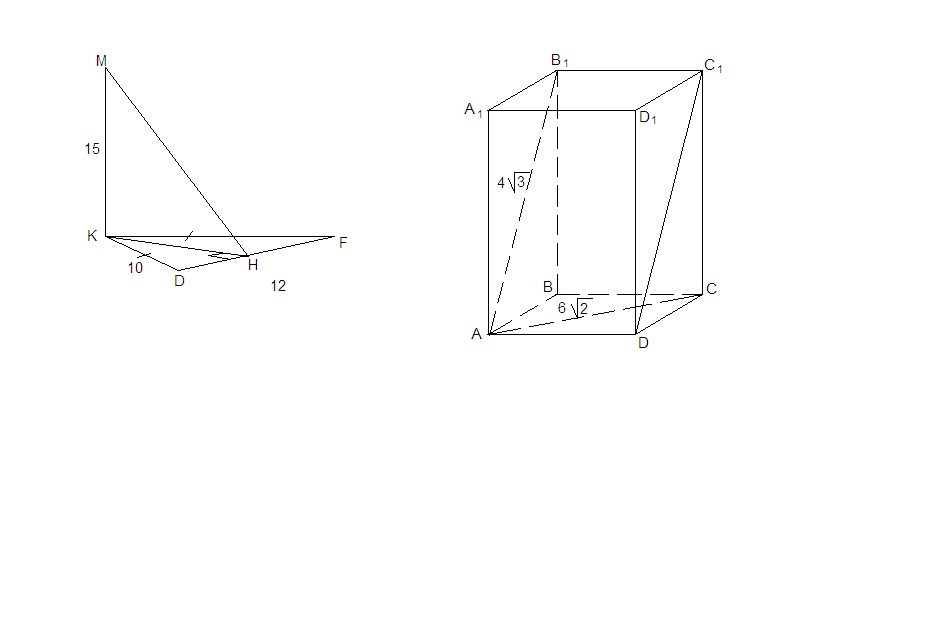
Через вершину К треугольника DKF проведена прямая KM, перпендикулярная к плоскости треугольника. 
Известно, что KM = 15см, DK = FK = 10 см, DF = 12 см. 
Найдите расстояние от точки M до прямой DF.


Дан прямоугольный параллелепипед ABCDA1B1C1D1. Найдите двугранный угол B1ADB, если ABCD - квадрат, если AC=6 корней из 2 (cм), AB1= 4 корня из 3 (cм).

Answer 1

1. Проведем КН⊥DF.  ΔDKF равнобедренный, значит КН - высота и медиана.
DH = HF = 6 см.
КН - проекция наклонной МН на плоскость DKF, значит, МН⊥DF по теореме о трех перпендикулярах.
МН - искомое расстояние.
ΔDKH: ∠KHD = 90°, по теореме Пифагора
KH = √(KD² - HD²) = √(100 - 36) = √64 = 8 (см)

ΔКМН: ∠MKH = 90°, по теореме Пифагора
MH = √(MK² + KH²) = √(225 + 64) = √289 = 17 (см)

2. ВА⊥AD, BA - проекция наклонной В₁А на плоскость основания. Значит, В₁А⊥AD по теореме о трех перпендикулярах.
∠В₁АВ - линейный угол двугранного угла В₁АDB - искомый.

Так как ABCD квадрат, его сторона АВ = АС/√2 = 6 (см)
Δ В₁АВ: ∠В₁ВА = 90°,
cos∠В₁АВ = AB/AВ₁ = 6/(4√3) = √3/2
⇒ ∠В₁АВ = 30°