Предмет: Алгебра,
автор: samurobro
Даю 40 баллов. Задание на фотографии
Приложения:
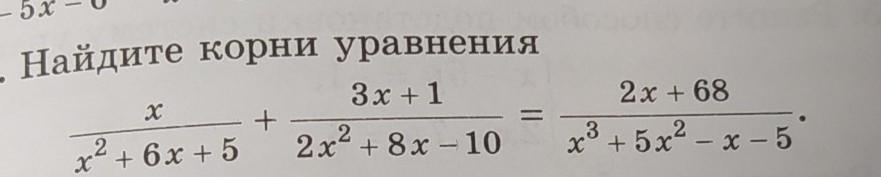
Ответы
Автор ответа:
0
предварительно разложим на множители все знаменатели
х²+6х+5=0; по Виету х=-1; х=-5⇒х²+6х+5=(х+1)(х+5)
2х²+8х-10=0; 2*(х²+4х-5)=0, по Виета х=1; х=-5⇒2х²+8х-10=2*((х-1)(х+5);
х³+5х²-х-5=х²(х+5)-(х+5)=(х²-1)(х+5)=(х-1)(х+1)(х+5);
приедем к общему знаменателю
2(х-1)(х+1)(х+5); учитывая после этого, что х≠±1; х≠-5, решим полученное уравнение.
х/(х+1)(х+5)+(3х+1)/(2*(х-1)*(х+5)=(2х+68)/((х+1)(х-1)(х+5))
(2х(х-1)+(3х+1)(х+1)-2*68)/(2*(х-1)(х+1)(х+5))=0
2х(х-1)+(3х+1)(х+1)-2*68-4х=0
2х²-2х+3х²+4х+1-2*68-4х=0
5х²-2х-135=0
х=(1±√(1+675))/5=(1±26)/5;х=-5, , т.к. не входит в ОДЗ,
х=5.4
Ответ 5.4
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: mgkoshyk
Предмет: Математика,
автор: yula2742
Предмет: Другие предметы,
автор: GARTENOFF1
x
x
2
+
6
x
+
5
+
3
x
+
1
2
x
2
+
8
x
−
10
=
2
x
+
68
x
3
+
5
x
2
−
x
−
5
, решив его относительно
x
.
x
=
27
5