Предмет: Геометрия,
автор: SevaCatic
ДАМ 90 БАЛЛОВ ЗА ПОДРОБНОЕ РЕШЕНИЕМ С ОБЪЯСНЕНИЕМ
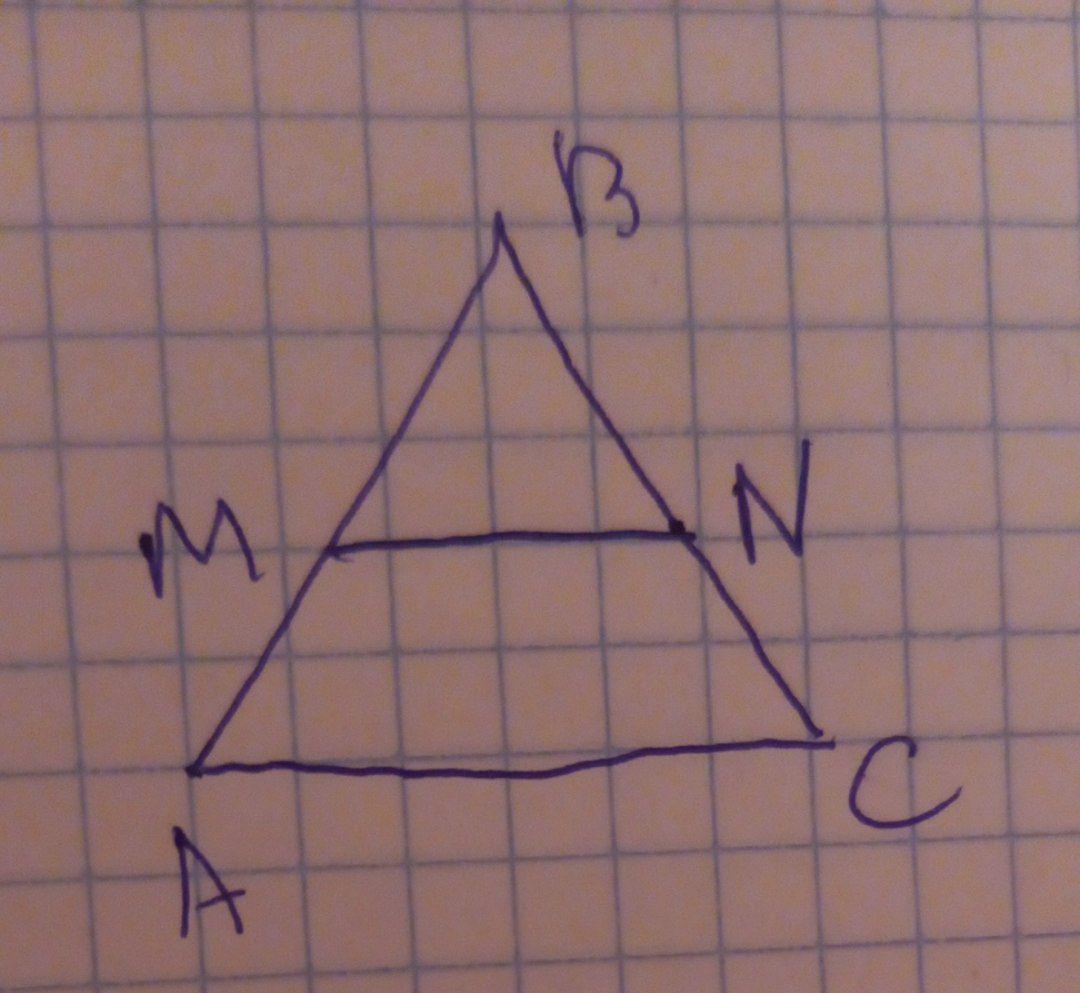
В треугольнике ABC, AM=MB,
BN=NC и MN+AC=24 см.
Найдите сторону AC.
Ответы:
А) 8 см
B) 16 см
C) 18 см
D) 9 см
Приложения:
Ответы
Автор ответа:
3
Ответ:
Объяснение:
MN - средняя линия треугольника АВС. MN=AC/2;
AC/2+AC=24
3AC=48
AC=48/3=16 см.
Автор ответа:
5
Ответ: АС=16 см .
Так как АМ=МВ , то точка М - середина стороны АВ . Аналогично , из равенства BN=NC следует, что N - cередина стороны ВС .
Значит, MN - средняя линия треугольника .
По свойствам средней линии треугольника MN || AC и MN=1/2 * AC , то есть MN - половина стороны АС . Значит, АС=2* MN .
MN+AC=MN+2*MN=3*MN , 3*MN=24 cм ⇒ MN=24:3 , MN=8 см .
АС=2*MN=2*8=16 cм .
Похожие вопросы
Предмет: Английский язык,
автор: денис639
Предмет: Другие предметы,
автор: диана0089
Предмет: Русский язык,
автор: Незнайка064
Предмет: Геометрия,
автор: zlatabereza