Предмет: Геометрия,
автор: prostochelovek680
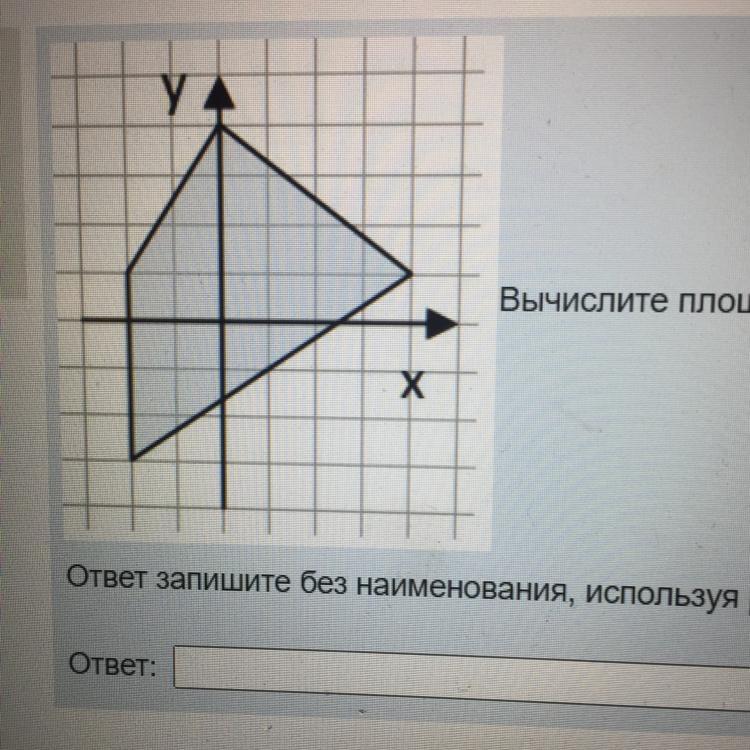
вычислите площадь закрашенной фигуры
Приложения:
Ответы
Автор ответа:
2
Ответ:
21ед²
Объяснение:
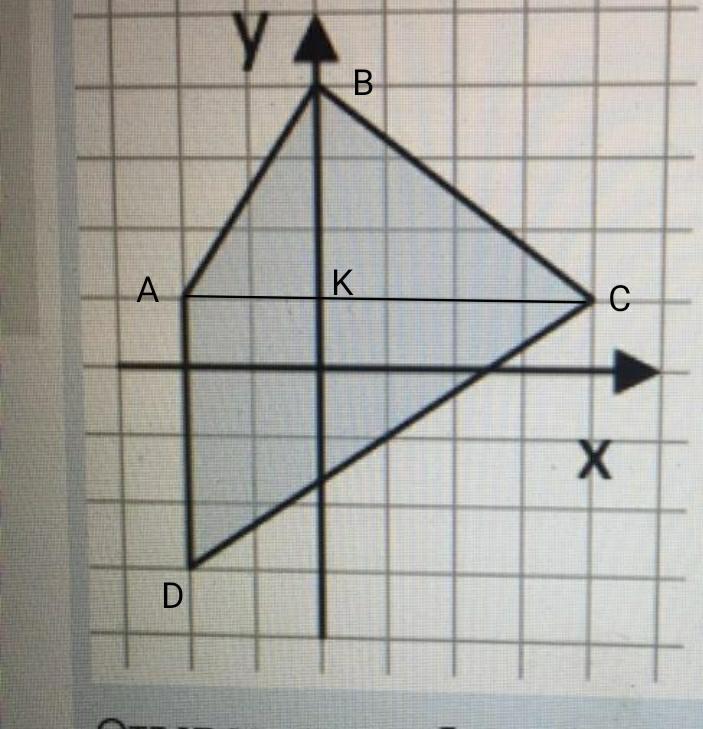
S(∆ABC)=AC*BK/2=6*3/2=9 ед²
S(∆DAC)=DA*AC/2=4*6/2=12ед
S(ABCD)=S(∆ABC)+S(∆DAC)=9+12=21ед²
Приложения:
Аноним:
Ваше предложение неправильно.
https://prntscr.com/26c68dc
https://prntscr.com/26c68vv
Четырехугольник вершины которого принадлежат сторонам прямоугольника. И две из находятся паралельно друг другу дают один треугольник основанием которого является сторона прямоугольника, а высота каждого из этих треугольников является тоже стороной прямоугольника.
Как если бы треугольник был в прямоугольнике с основанием прямоугольника.
эх!!!...такую песню "дядь" испортил!!!...))) ну и ладно!... другую споем!!! спасибо за общение... весьма приятное!!!
https://prntscr.com/26c69x8.
Ладно...
Я готова выдать следующее. Площадь четырехугольника вписанного в прямоугольник равна половине площади прямоугольника, если две противоположные вершины четырехугольника лежат на одной прямой параллельной одной из сторон данного прямоугольника.
согласен сразу. это сводится к утверждению: треугольник в прямоугольнике у которого совпадают стороны, и вершина треугольника лежит на противоположной стороне прямоугольника.
Автор ответа:
1
Ответ: S=21 ед² .
Длина клеточки = 1 единица длины. Площадь одной клеточки = 1 ед².
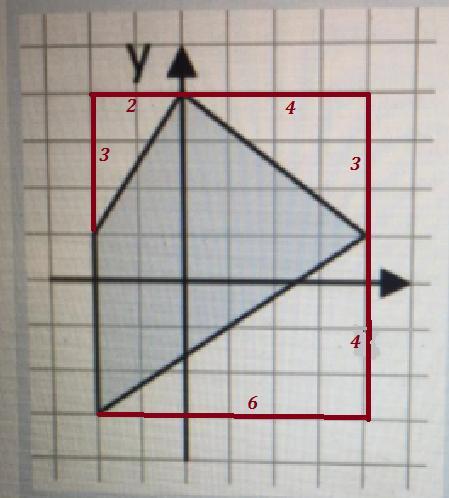
Достроим прямоугольник, как показано на рисунке . Площадь его равна 7*6=42 ед² .
Вычтем из площади прямоугольника площади трёх прямоугольных треугольников :
Площадь заданной фигуры равна :
ед² .
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: natulya1988
Предмет: Русский язык,
автор: somava1985
Предмет: Русский язык,
автор: kdkkdkddkdkkd
Предмет: Английский язык,
автор: Аноним