Предмет: Алгебра,
автор: nurcanpashali
В какой четверти расположена вершина параболы у=(х+3)²+5 ?
Дайте ответ с объяснением, пожалуйста...
Ответы
Автор ответа:
5
Ответ:
II четверть
Объяснение:
y = (x + 3)² + 5;
(раскрываем скобки по формуле (a+b)² = a² + 2ab + b²)
y = x² + 6x + 9 + 5;
y = x² + 6x + 14;
y = ax² + bx + c - формула параболы.
у нас получилось: x² + 6x + 14, значит:
a = 1; b = 6; c = 14.
Формула координаты x₁ вершины параболы: x₁ = -b/2a = -6/2•1 = -3
Подставляем в уравнение: y₁ = 9 - 6•3 + 14 = 9 - 18 + 14 = 5
Координаты вершины: (-3; 5) - значит II четверть.
nurcanpashali:
Огромное вам спасибо
Автор ответа:
1
Объяснение:
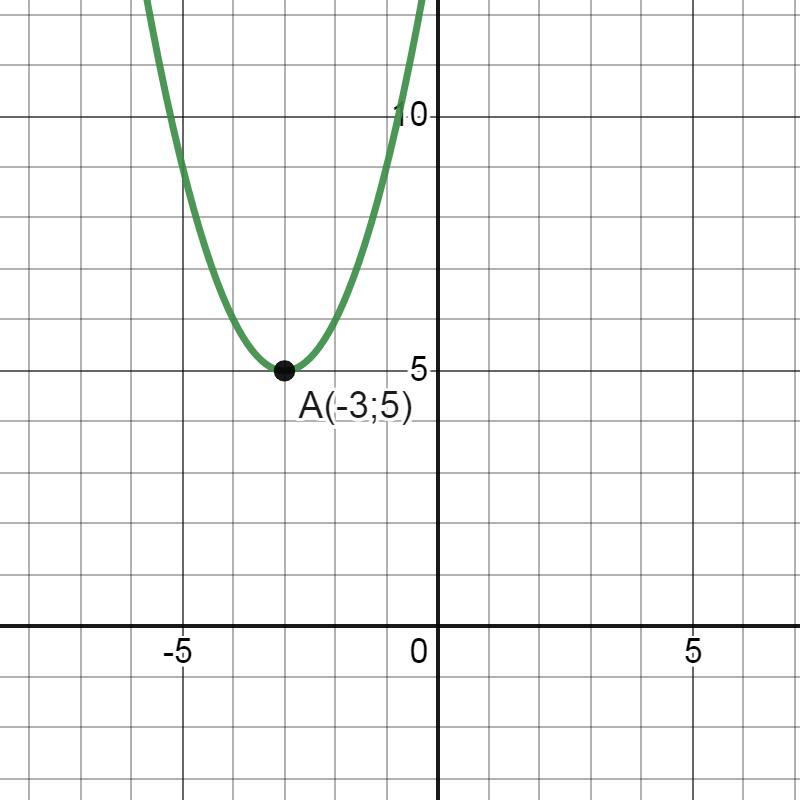
Ответ: вершина параболы у=(х+3)²+5 c координатами А(-3;5)
находится во второй четверти.
Приложения:
Большое спасибо
Удачи.
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: Вероника564
Предмет: Русский язык,
автор: мария1422
Предмет: Математика,
автор: ancelika95
Предмет: Химия,
автор: weapona34