Question

CРОЧНО!!!!!!!Составить уравнение линии, каждая точка M которой отстоит от точки А(1; 0) на расстояние в пять раз меньшее, чем от прямой x=8.

Answer 1

Ответ:

24·x²–34·x+25·y²=39

Пошаговое объяснение:

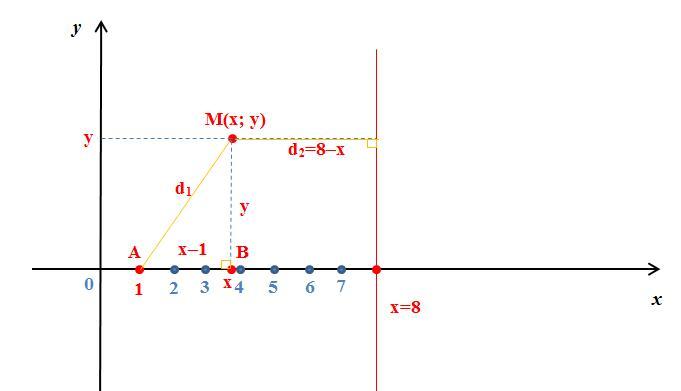
Пусть (x; y) координаты точки M, то есть M(x; y), d₁ – расстояние от точки M(x; y) до точки А(1; 0), а d₂ – расстояние от точки M(x; y) до прямой x=8.  

Проекцией точки M(x; y) на ось Ох будет точкой В(x; 0) (см. рис). Тогда расстояние d₁ можем найти из прямоугольника треугольника AMB с катетами  

АВ = (х–1) и ВM = у.

Применим теорему Пифагора: d₁²=(х–1)²+у².

Далее, расстояние от точки M(x; y) до прямой x=8 равно

d₂=|8–х|.

По условию задачи  

5·d₁ = d₂ или 25·d₁² = d₂².

Получим уравнение:

25·((х–1)²+у²) = (8–х)².

Упростим уравнение:

25·x²–50·x+25+25·y²–x²+16·x=64

24·x²–34·x+25·y²=39.