Предмет: Математика,
автор: denissro
Помогите решить рациональное неравенство!!
Приложения:
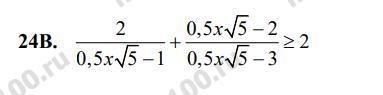
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: ana41
Предмет: Алгебра,
автор: leila0678
Предмет: Биология,
автор: Jeddy41