Question

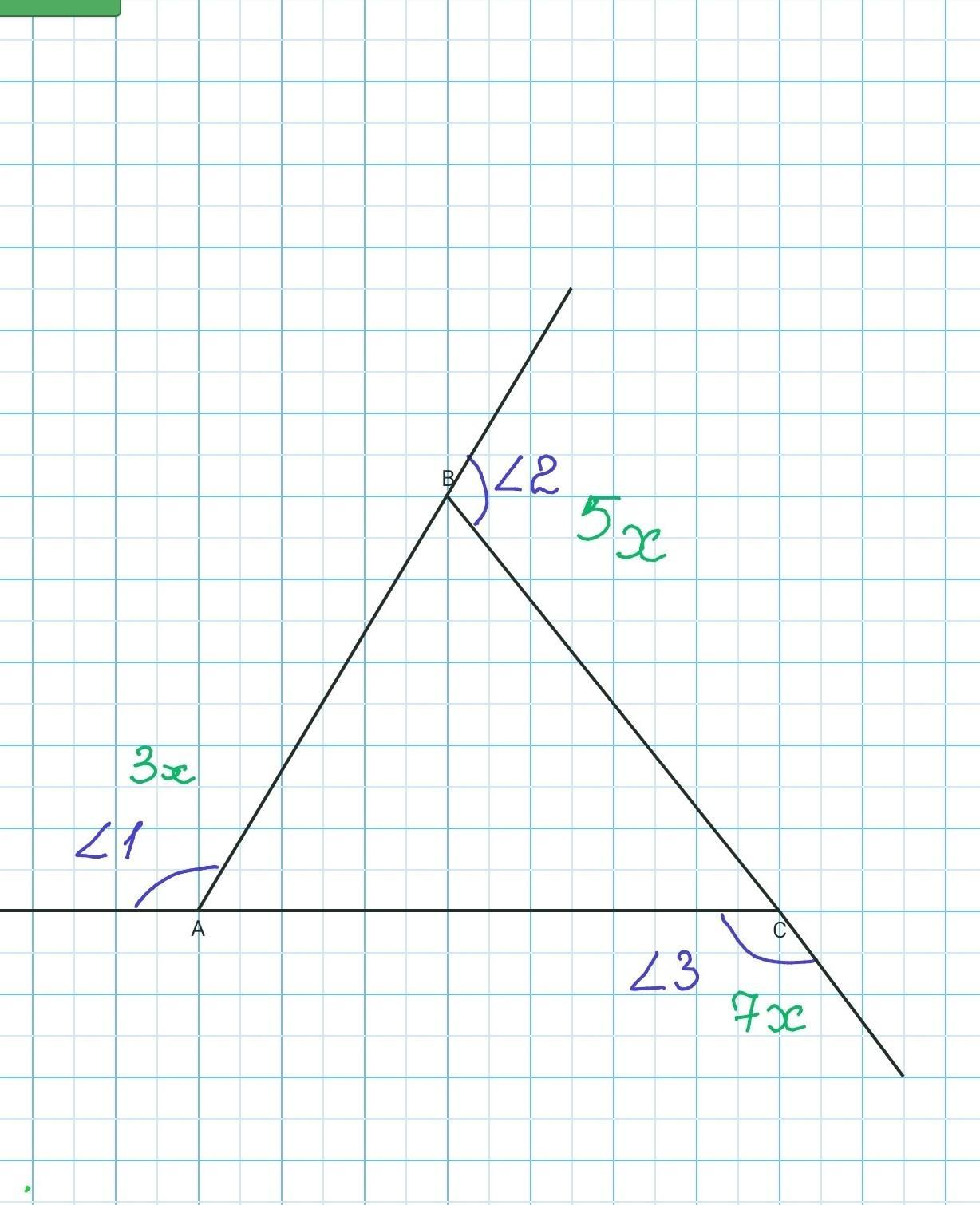
Найдите внутренние углы треугольника, если внешние углы пропорциональны числам 3, 5, 7.

Answer 1

Ответ:

108°, 60°, 12°

Объяснение:

Внешний угол треугольника равен сумме двух внутренних углов не смежных ним:

<1=<В+<С

<2=<А+<С

<3=<А+<В

отсюда сумма внешних углов треугольника взятых по одному при каждой вершине равна:

<1+<2+<3=<В+<С+<А+<С+<А+<В=2(<А+<В+<С)

Так как сумма углов треугольника равна 180 градусов то <А+<В+<С=180°.

Значит <1+<2+<3=2×180°=360°

Пусть:

<1=3х

<2=5х

<3=7х

Составляем уравнение:

3х+5х+7х=360

15х = 360

х = 24

<1=3х=3×24=72°

<2=5х=5×24=120°

<3=7х=7×24=168°

Так как внешний угол треугольника - это угол смежный с внутренним углом треугольника, а сумма смежных углов равна 180° то

<А= 180°-<1=180°-72°=108°

<В=180°-<2=180°-120°=60°

<С=180°-<3=180°-168°=12°