Question

найти площадь фигуры ограниченной линиями f(x)=x+5, g(x)=6/x, x=-2, x=6 и осью 0x

Answer 1

Ответ:

Площадь фигуры ограниченной линиями f(x)=x+5, g(x)=6/x, x=-2, x=6 и осью 0x равна (16,5 +6 ln6) ед.²

Объяснение:

Требуется найти площадь фигуры ограниченной линиями f(x)=x+5, g(x)=6/x, x=-2, x=6 и осью 0x.

Площадь фигуры найдем по формуле:

$\displaystyle \boxed { S=\int\limits^a_b {(f_2(x)} -f_1(x))\, dx}$

Дано:

$\displaystyle f(x)=x+5;\;\;\;\;\;g(x)=\frac{6}{x};\;\;\;\;\;x=-2;\;\;\;\;\;x=6;\;\;\;\;y=0$

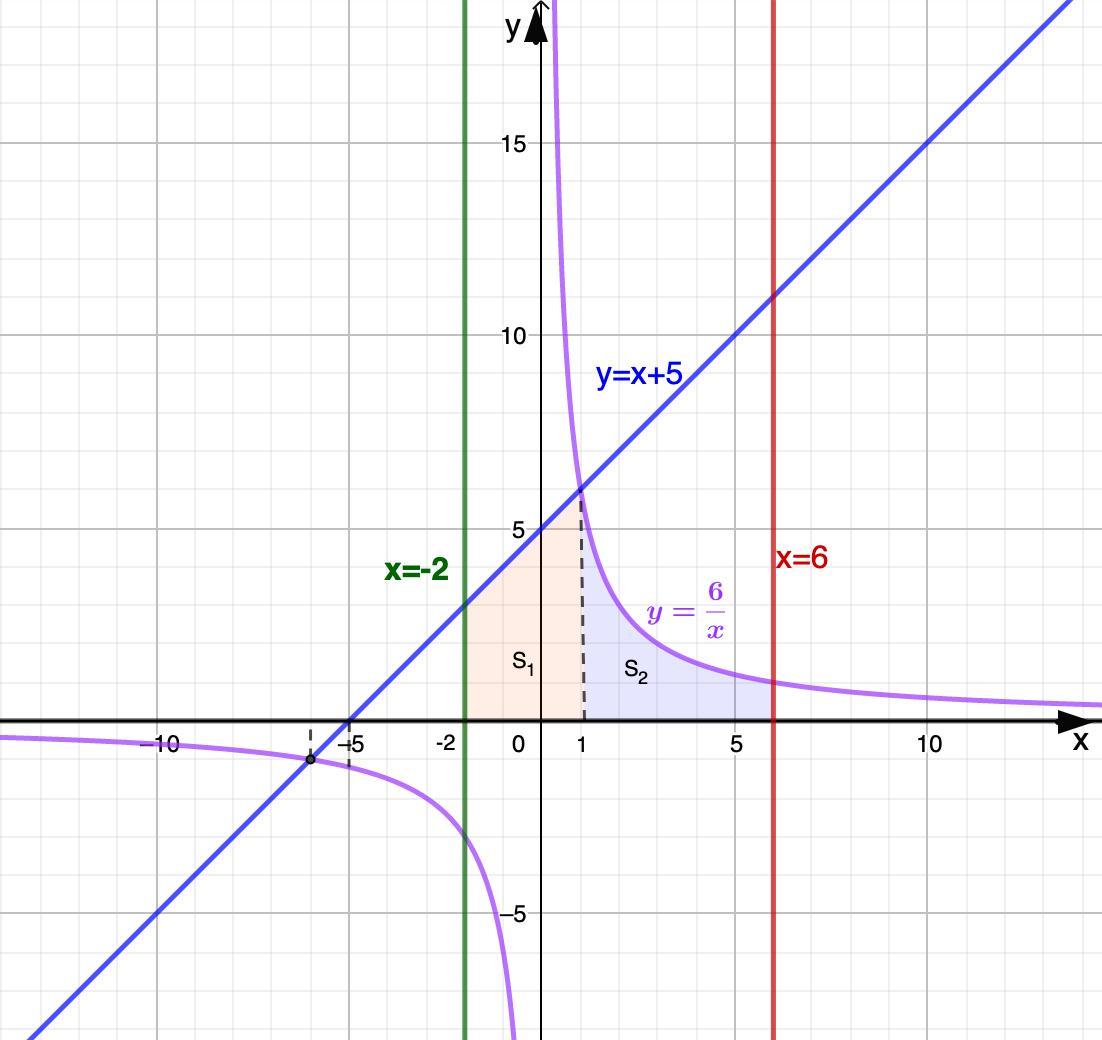
Построим графики и определим область, которая ограничена данными линиями.

1. $\displaystyle y = x+5$

-линейная функция, график прямая.

Для построения достаточно две точки:

х = -5, у=0;

х = 1, у=6.

Строим график.

2. $\displaystyle y=\frac{6}{x}$

-функция обратной пропорциональности, график гипербола, расположенная в первой и третьей четвертях.

Возьмем четыре точки:

х = 1, у = 6;

х = 2, у = 3;

х = 3, у = 2;

х = 6, у = 3.

Строим одну ветвь гиперболы. Вторую строим симметрично начала координат.

3. Точки пересечения данных графиков:

(1; 6) и (-6; -1).

4. Видим, что искомая площадь состоит из двух площадей:

$\displaystyle S=S_1+S_2$

5. Найдем S₁.  

Линия сверху f₂(x) = x+5, снизу f₁(x) = 0, слева b = -2, справа a = 1.

$\displaystyle S_1=\int\limits^1_{-2} {(x+5-0)} \, dx =\left({\frac{x^2}{2}+5x }\right)\;\Big|^1_{-2}=\\\\=\left(\frac{1}{2}+5\right)-\left(\frac{4}{2}+5*(-2)\right)=5\frac{1}{2}-2+10 =13,5$

6. Найдем S₂.

f₂(x) = 6/x,  f₁(x) = 0, b = 1,  a = 6.

$\displaystyle S_2=\int\limits^6_1 {\left(\frac{6}{x}-0\right) } \, dx =6ln\;|x|\;\Big|^6_1=\\\\=6(ln\;6-ln\;1)=6\;ln\;6$

7. S = S₁ +S₂ = 13,5 + 6 ln6 (ед²)