Предмет: Геометрия,
автор: mahmadzodahafizullo
Даны точки A(1;0;-1), B(0;2;–3), C(2;4;-2), D(-2;m;2). Найдите наименьшее значение параметра m, при котором объём тетраэдра DABC равен 6.
Ответы
Автор ответа:
0
Ответ:
m=3
Объяснение:
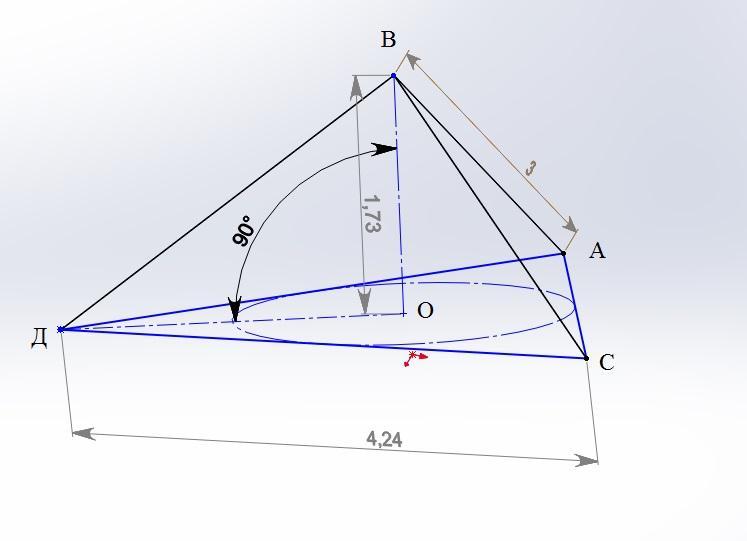
АВ=ВС≠АС ⇒ АВС боковая грань тетраэдра
АС=ДС=ДА=4,24 стороны Δ основания
Боковые ребра АВ=ВС=3
Вершина тетраэдра В
Высота тетраэдра ВО ⊥ основанию, т. О находится в центре вписанной в Δ АСД основания. Исходя из этих условий
|ДС|=√(ДСх+ДСу+ДСz)=4,24
|ДА|=√(ДАх+ДАу+ДАz)=4,24 найдем координаты Д(-2;3;-1)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ленок8160
Предмет: Русский язык,
автор: 1алекс89ей
Предмет: Русский язык,
автор: shdariya
Предмет: Алгебра,
автор: girlokay
Предмет: Математика,
автор: sofia34545