Предмет: Математика,
автор: allakhverdievagulya5
Помогите пж. РЕШИТЕ УРАВНЕНИЕ
Приложения:

ВикаБач:
у=Сosx. Дальше совсем просто.
ну это смотря для кого))
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Применим основное тригонометрическое тождество и заменим
Пусть . Тогда уравнение принимает вид:
Условию удовлетворяет
Приложения:
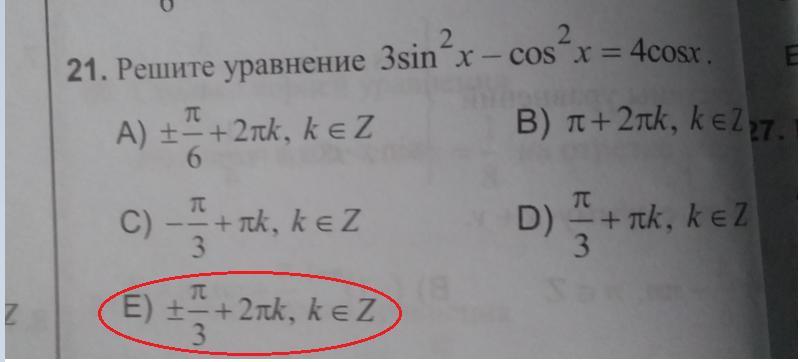
Похожие вопросы
Предмет: Окружающий мир,
автор: petkoglo75
Предмет: Русский язык,
автор: nadezhda142
Предмет: Русский язык,
автор: Отличник0707
Предмет: История,
автор: Аноним
Предмет: Биология,
автор: xzxz89838