Предмет: Алгебра,
автор: alex2864

Найти область значений функций.
Ответы
Автор ответа:
1
Ответ:
, ОДЗ:
.
Определение модуля:
Поэтому заданную функцию можно записать в виде :
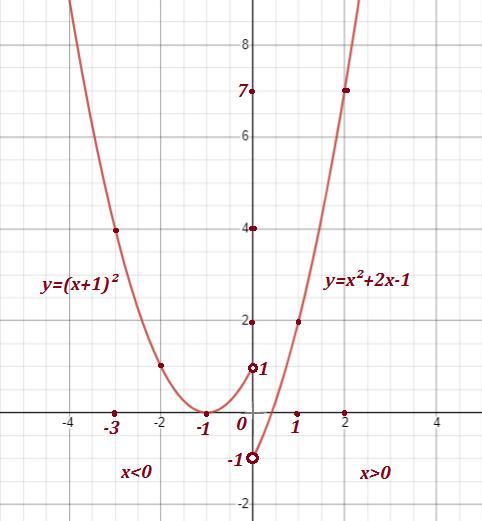
Построим график функции . Точки , через которые проходит график: (-3:4) , (-2;1) , (-1,0) , (1;2) , (2;7) .
По графику определим, что область значений функции
.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Отличник0707
Предмет: Английский язык,
автор: kolrolke
Предмет: Русский язык,
автор: antixomirova
Предмет: Другие предметы,
автор: kosharavelikai123