Предмет: Геометрия,
автор: Аноним
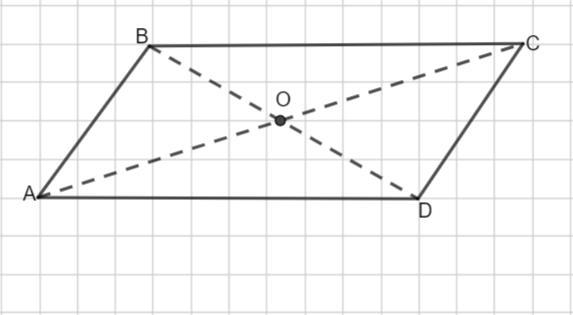
Даны вершины параллелограмма ABCD: A(1;-2;2); B(1;4;0); C(-4;1;1). Найти координаты точки D.
Ответы
Автор ответа:
2
Ответ:
D(-4; -3; 3) .
Объяснение:
A(1;-2;2)
B(1;4;0)
C(-4;1;1)
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Найдем координаты точки О - середины диагонали АС. Для этого воспользуемся формулами нахождения координат середины отрезка.
Точка О является серединой и диагонали BD.
Найдем абсциссу точки D
Найдем ординату точки D
Найдем аппликату точки D
D(-4; -3; 3)
Приложения:
Аноним:
Спасибо Вам, радость моя!
Похожие вопросы
Предмет: Окружающий мир,
автор: вика1862
Предмет: Русский язык,
автор: madinbesk
Предмет: Русский язык,
автор: LYUDsusicheren
Предмет: Математика,
автор: missbi838
Предмет: Алгебра,
автор: dmerei