Question

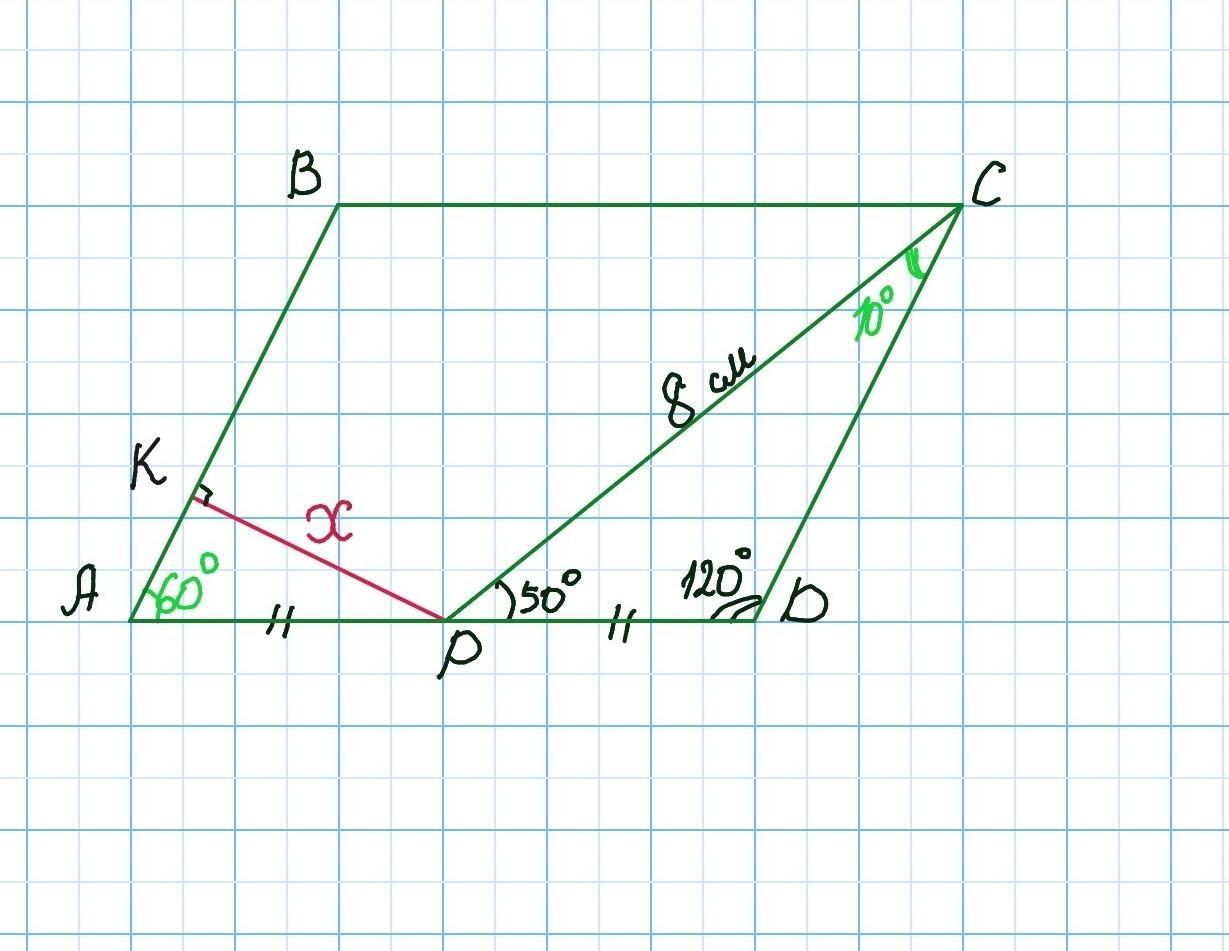
Точка P — середина стороны AD параллелограмма ABCD. Известно, что PC=8 см, ∠CPD = 50°, ∠D = 120° . Найдите расстояние от P до стороны AB.

Answer 1

Ответ:

8sin10° или примерно 1,39 см

Объяснение:

Рассмотрим треугольник РCD. Так как сумма углов треугольника равна 180 градусов угол C равен:

180°-50°- 120°=10°

По теореме синусов найдём сторону PD:

$\dfrac{PD}{ \sin(10) } = \dfrac{PC}{ \sin(120) } \\ \\ PD = \dfrac{PC \times \sin(10) }{ \sin(120) } = \dfrac{8 \times \sin(10) }{ \frac{ \sqrt{3} }{2} } = \dfrac{16 \sin(10) }{ \sqrt{3} }$ см

Опустим перпендикуляр РК на сторону AB. РK искомое расстояние от Р до АВ.

Рассмотрим прямоугольный треугольник AРК(<К=90°).

АР=PD - по условию, <KAP=180°-<D=180°-120°=60° - как соседние углы параллелограмма.

$x = AP \times \sin(60) = \dfrac{16}{ \sqrt{3} } \sin(10) \dfrac{ \sqrt{3} }{2} = 8 \sin(10)$см