Предмет: Геометрия,
автор: tashlanovaana
В основании пирамиды лежит треугольник, одна из сторон которого равна 4, а противолежащий ей угол равен 30 градусов. Боковые ребра перамиды равны 5. Найдите расстояние от центра описанного около пирамиды шара до плоскости основания.
siestarjoki:
7/6
Ответы
Автор ответа:
1
Основание ABC, AB=4, ∠C=30°
H - центр описанной окружности.
AB/sinC =2AH (т синусов) => AH=4
Если боковые ребра пирамиды равны, то вершина падает в центр описанной окружности основания.
SH⊥(ABC)
SH=√(SA^2-AH^2) =3 (т Пифагора)
О - центр описанной сферы.
OABC - пирамида с равными боковыми ребрами, следовательно ее вершина также падает в центр H.
OH⊥(ABC)
S-H-O на одной прямой.
В плоскости ASO.
OS=OA, О на серединном перпендикуляре к SA.
M - середина SA, SM=5/2
△SOM~△SAH
SO/SA=SM/SH => SO/5=5/2*3 => SO=25/6
OH =SO-SH =25/6 -3 =7/6
Приложения:
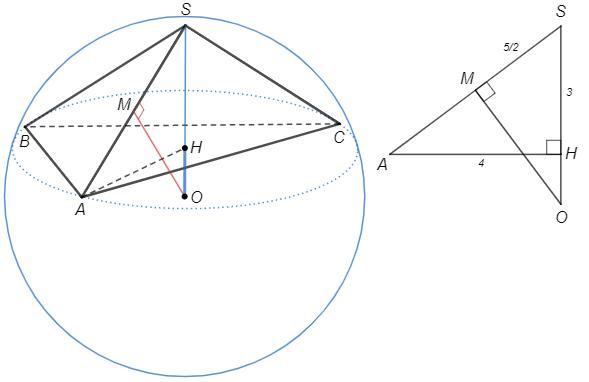
Центр описанной сферы - пересечение перпендикуляров через центры описанных окружностей граней.
В основании пирамиды лежит треугольник, одна из сторон которого равна 4, а противолежащий ей угол равен 30 градусов. Боковые ребра перамиды равны 5. Найдите расстояние от центра описанного около пирамиды шара до плоскости основания.
Похожие вопросы
Предмет: Русский язык,
автор: eli22
Предмет: Английский язык,
автор: Кочкарев
Предмет: Русский язык,
автор: ajgul2030
Предмет: Алгебра,
автор: animeshnik64
Предмет: Русский язык,
автор: farangiz052006