Предмет: Математика,
автор: poladov666
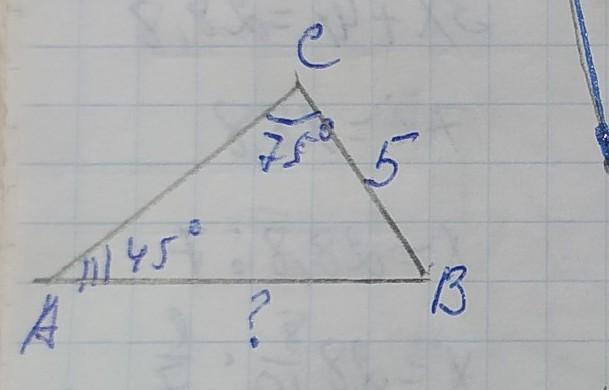
Найдите сторону AB треугольника ABC ,если BC=5см,угол C=75°,угол A=45°
Ответы
Автор ответа:
0
Ответ:
АВ=2,5(√3+1)=2,5√3+2,5 см
Пошаговое объяснение:
Воспользуемся теоремой синусов:
перемножим крест на крест:
АВ×sinA=BC×sinC
АВ×sin45°=BC×sin75°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Ritoochkaa2604
Предмет: Русский язык,
автор: niash
Предмет: Русский язык,
автор: apriatkina34Sasha
Предмет: Математика,
автор: gorik2001pro123