Предмет: Математика,
автор: jopa2288
Помогите решить задачи !!!
Приложения:
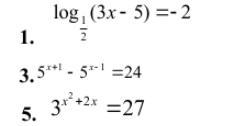
Ответы
Автор ответа:
1
ответ;
пощаговый о__________
Приложения:

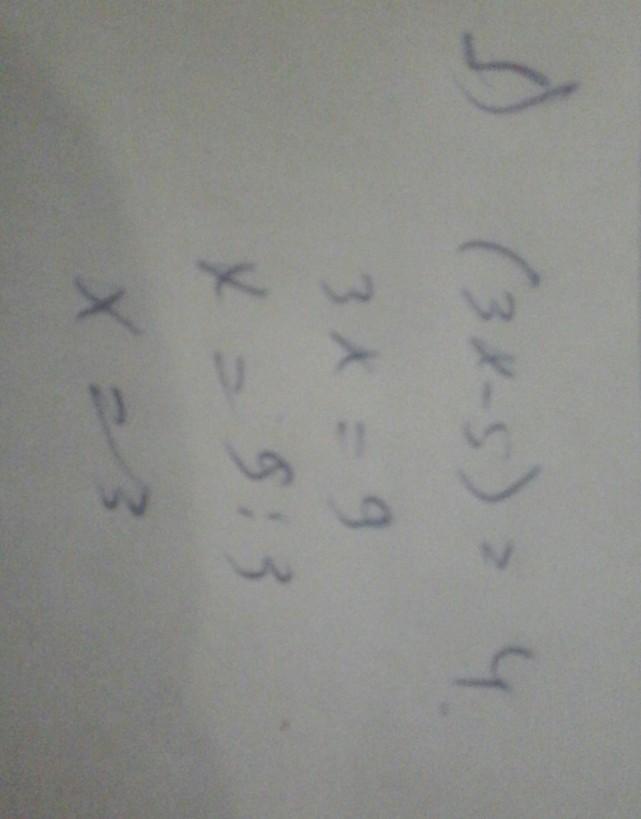

Автор ответа:
1
Ответ:
По определению логарифма имеем: ,
Воспользуемся свойствами: .
Похожие вопросы
Предмет: Русский язык,
автор: glebka7
Предмет: Русский язык,
автор: MRSAB
Предмет: Русский язык,
автор: loki29
Предмет: Биология,
автор: Аноним
Предмет: Русский язык,
автор: 3Андроп1