Question

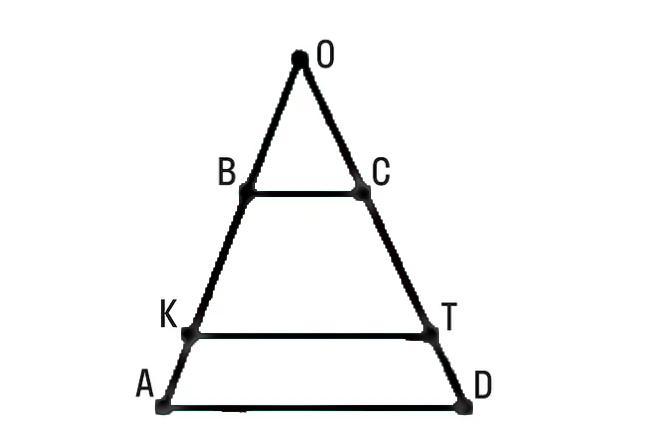
Продолжение боковых сторон трапеции ABCD, BA||AD пересекаются в точке O. Прямая KT||BC, BKЭAB, DTЭCD. BK=4,AK=3,CT=8, OC=12. Найди DT и OB

Answer 1

Ответ:

ВО=6

DT=6

Объяснение:

ΔВСО, ΔКТО И ΔАДО подобны по трем равным углам

к подобия СТ/ВК=8/4=2

ВО=ОС/к=12/2=6

DT=3*к=3*2=6