8 класс, геометрия, тема "Параллелограмм"
ABCD - параллелограмм
AM и AN - медианы
AMN - равносторонний треугольник
Найдите углы параллелограмма
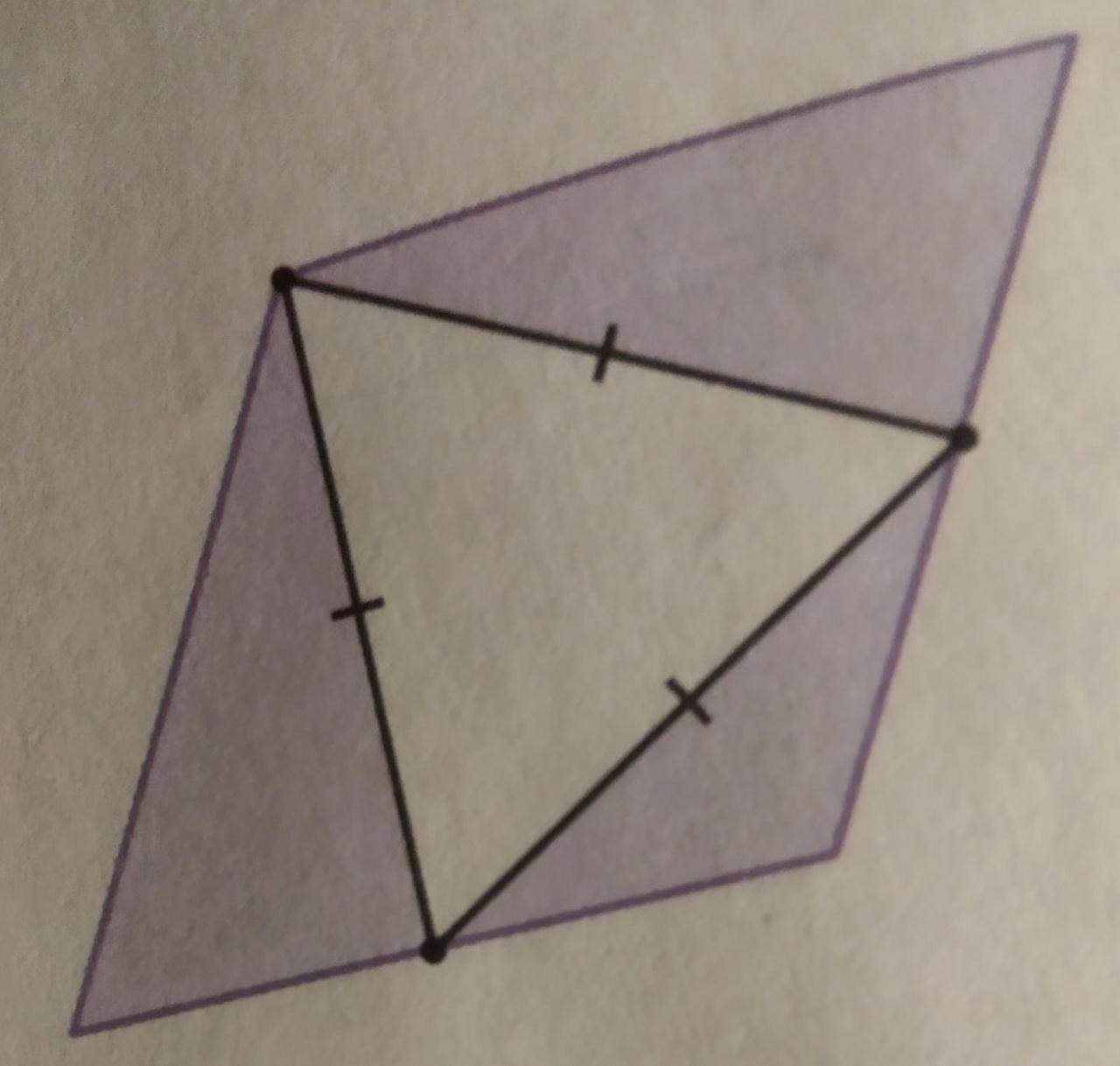
Ответы
Решение:
ABCD - параллелограмм (по условию)
АМ и АN - медианы (по условию)
AMN - равносторонний треугольник (по условию).
Рассмотрим треугольник AMN:
∆AMN - равносторонний, значит, все углы по 60°.
Рассмотрим треугольник MNC:
Угол NMC равен 180°- 90°- 60°=30° ( Т.к угол AMD и угол AMC смежные, угол AMD - прямой, угол AMN=60°(т.к равносторонний треугольник), все вычитаем).
Угол MNC равен 180°-90°-60°=30° (Т.к углы AND и ANC смежные, угол AND - прямой, ANM=60°(равносторонний треугольник), все вычитаем).
Углы при основании NMC и MNC равны, значит, ∆MNC - равнобедренный треугольник.
Угол MCN = 180° - 30° - 30°= 120°.
Рассмотрим параллелограмм ABCD:
Угол MCN (или угол C)=120°, т.к это параллелограмм, то противоположные углы равны → угол А равен 120° соответственно.
Также в параллелограмме сумма соседних углов равна 180°→ углы С и D равны 180°-120°=60°.
Ответ: 120°;60°