Предмет: Алгебра,
автор: isakovainna23
Помогите, пожалуйста, решить нерванство методом замены множителей.
Приложения:
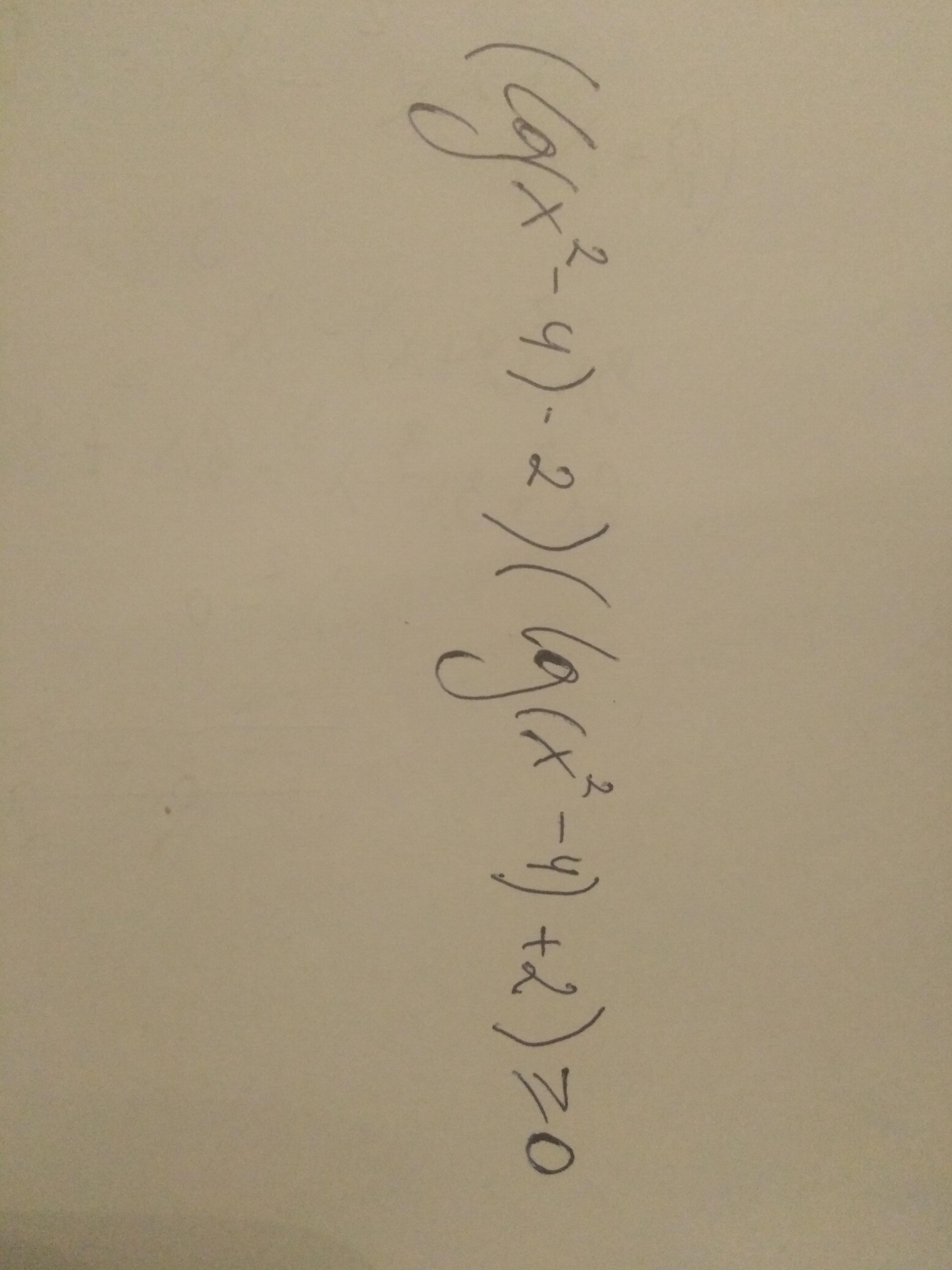
Ответы
Автор ответа:
4
Ответ:
Объяснение:
учитывая ODZ, получаем
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: petya33
Предмет: Українська мова,
автор: ivanka0307
Предмет: Русский язык,
автор: Aishatik12
Предмет: Уход за собой,
автор: Rexona2018