Предмет: Геометрия,
автор: bogdantejkin
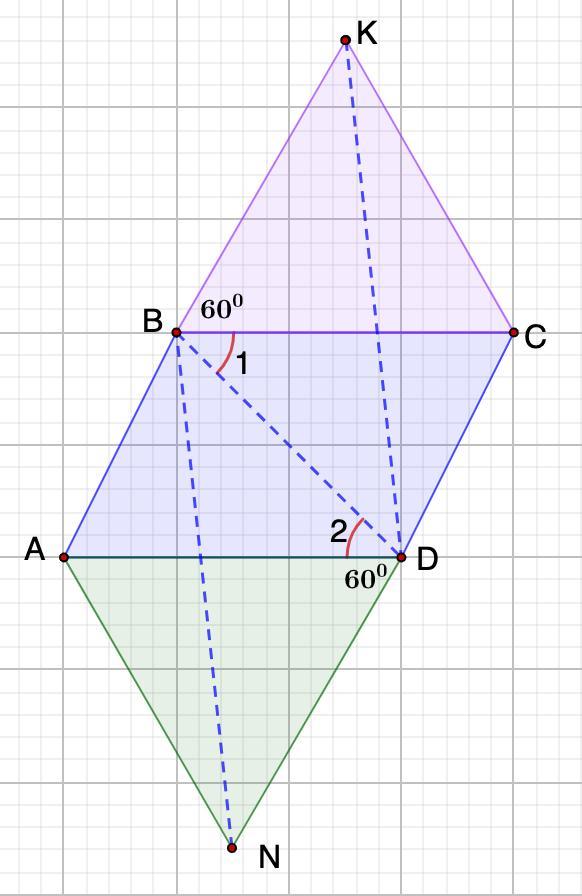
На сторонах параллелограмма ABCD построены равносторонние треугольники BKC и AND. Докажите, что BKDN — параллелограмм.
Ответы
Автор ответа:
1
Объяснение:
Дано: ABCD - параллелограмм.
ΔВКС и ΔAND - равносторонние.
Доказать: BKDN - параллелограмм.
Доказательство:
1. Рассмотрим ΔВКС и ΔAND - равносторонние.
- Противоположные стороны параллелограмма равны.
⇒ ВС = AD
⇒ ΔВКС = ΔAND (по трем сторонам, 3 признак)
⇒ BK = ND
2. ВС || AD (ABCD - параллелограмм)
∠1 = ∠2 (накрест лежащие при ВС || AD и секущей BD)
- В равностороннем треугольнике углы равны 60°.
⇒
∠DBK = ∠1 + 60°
∠BDN = ∠2 + 60°
⇒ ∠DBK + ∠BDN - накрест лежащие при BK и ND и секущей BD.
- Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.
⇒ BK || ND
- Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм.
⇒ BKDN — параллелограмм
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: nastenka990
Предмет: Русский язык,
автор: полька117
Предмет: Окружающий мир,
автор: veronikkot2016
Предмет: Музыка,
автор: vovabogdanov29
Предмет: Английский язык,
автор: aialim15544