Предмет: Алгебра,
автор: eva444786
ПОМОГИТЕ НАЙТИ ПРОИЗВОДНУЮ СЛОЖНОЙ ФУНКЦИИ.
Приложения:
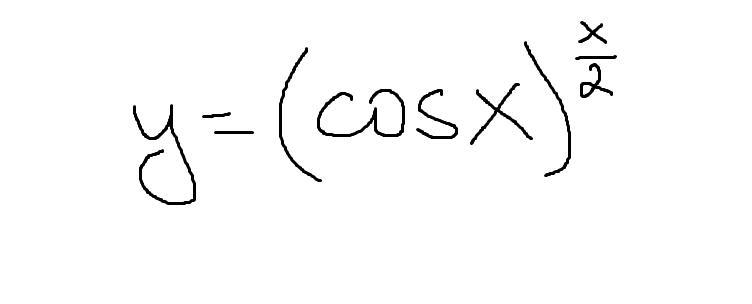
Ответы
Автор ответа:
1
Ответ:
Так как функция степенно-показательная, то применимо логарифмическое дифференцирование . Прологарифмируем заданное равенство и найдём производную от обеих частей полученного равенства, выразим у' .
Автор ответа:
0
Применяем основное логарифмическое тождество:
По формуле:
Похожие вопросы
Предмет: Русский язык,
автор: filya2016
Предмет: Английский язык,
автор: valera175
Предмет: Французский язык,
автор: ЛизаЗайчик
Предмет: Алгебра,
автор: milana95619
Предмет: Физика,
автор: bahsgsnzggsjhs