Предмет: Математика,
автор: 131211357
Вычислить несобственный интеграл или установить его расходимость.
Приложения:
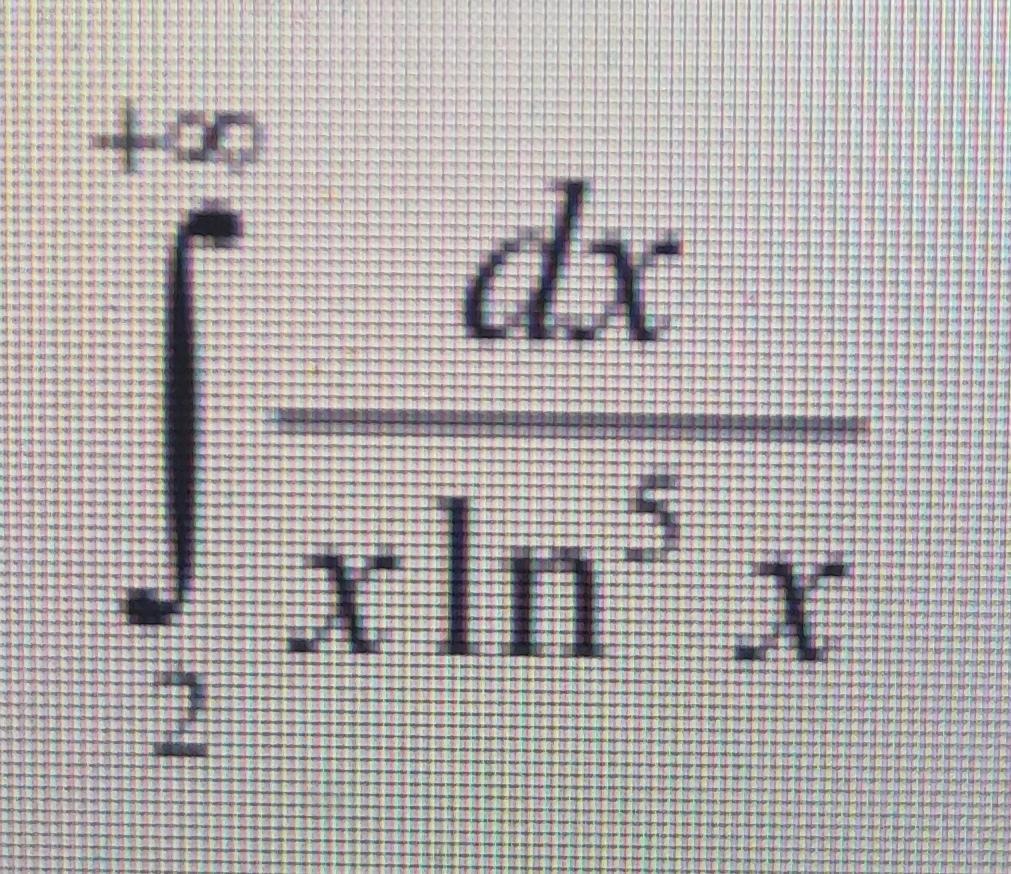
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Заменим в интеграле символ бесконечности на букву A и запишем в виде предела:
,
Произведём замену:
Заменим переменные в интеграле:
При подстановке вместо A бесконечности она оказывается в знаменателе и слагаемое с ней обращается в 0. У нас остаётся ещё одно слагаемое, показывающее сходимость данного интеграла. Именно оно и является ответом
Похожие вопросы
Предмет: Русский язык,
автор: supersavar20121
Предмет: Русский язык,
автор: HelloGuys1
Предмет: Русский язык,
автор: 777711
Предмет: Русский язык,
автор: 1233072