Предмет: Математика,
автор: pykpykovna
весь пример на фото. решение тоже желательно прислать им
Приложения:
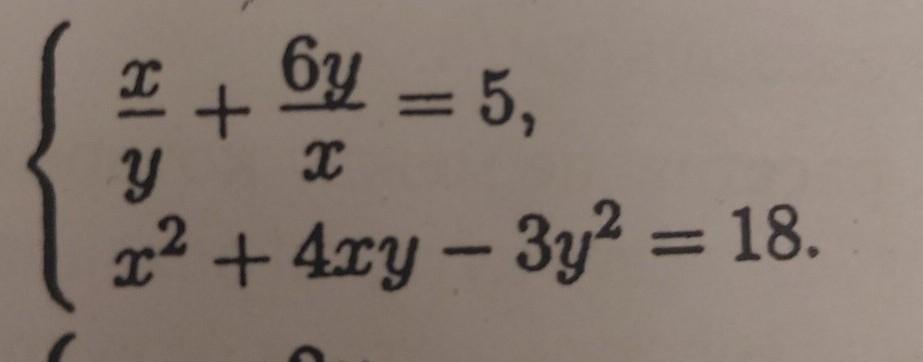
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Замена :
Тогда:
Решаем первое уравнение
Согласно теореме Виета
Решаем второе уравнение в случае когда
К замене:
Решаем второе уравнение в случае когда
К замене:
ОТВЕТ
Похожие вопросы
Предмет: Русский язык,
автор: kir2004ma
Предмет: Другие предметы,
автор: златка4
Предмет: Английский язык,
автор: Xima5
Предмет: Английский язык,
автор: Adema007
Предмет: Геометрия,
автор: radmir1234444