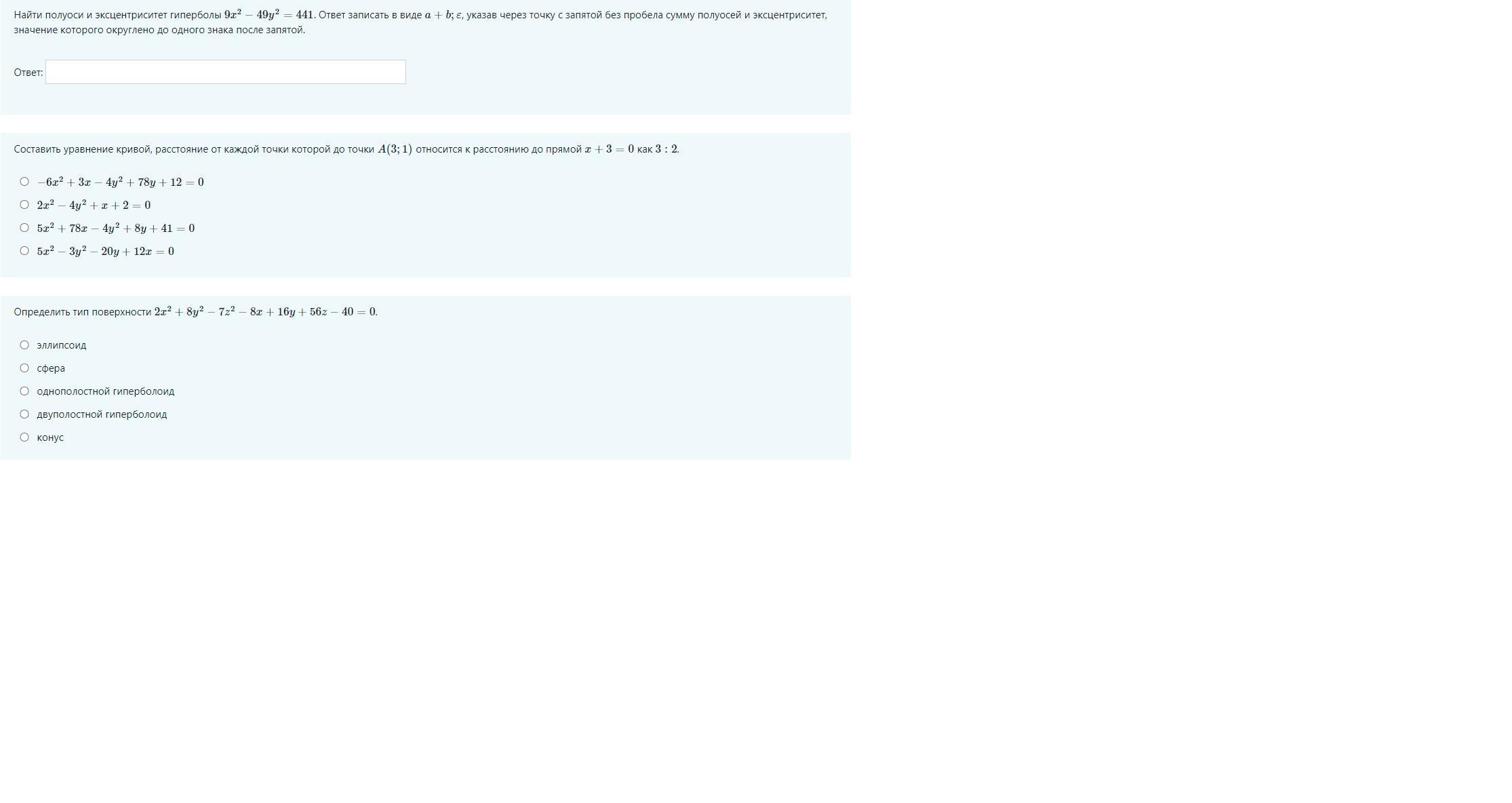
1. Найти полуоси и эксцентриситет гиперболы 9x^2−49y^2=441. Ответ записать в виде a+b;ε, указав через точку с запятой без пробела сумму полуосей и эксцентриситет, значение которого округлено до одного знака после запятой.
2. Составить уравнение кривой, расстояние от каждой точки которой до точки A(3;1) относится к расстоянию до прямой x+3=0 как 3:2.
3. Определить тип поверхности 2x^2+8y^2−7z^2−8x+16y+56z−40=0.
Подробнее во вложении
Ответы
1. 9x² - 49y² = 441
Разделим обе части уравнения на 441, получим
(9x²/441) - (49y²441) = 441/441
(х²/49) - (у²/9) = 1.
каноническое уравнение (х²/7²) - (у²/3² )= 1.
полуоси:
a =7, b = 3
Половина расстояния между фокусами - параметр с и он равен
с = √(a² + b²) = √(49+9 ) = √58 ≈7.6
Координаты фокусов:
Эксцентриситет гиперболы равен с/а ;
ε = √58/7=7.6/7≈1.0
a+b=7+3=10;
Ответ 10;1.0
2. отношение квадратов расстояний будет равно 9/4, пусть (x;y) -- точка кривой, квадрат её расстояния до А равен
(x−3)²+(y−1)² ;расстояние до прямой x+3=0 от точки (x,y) равно модулю разности абсцисс |x+3|. значит, 4((x−3)²+(y−1)²)=9(x+3)². упростим уравнение 4*(х²-6х+9+у²-2у+1)=9*(х²+ 6х+9);
9*х²+ 54х+81-4х²+24х-36-4у²+8у-4=0;
5х²+78х-4у²+8у+41=0- это третье уравнение
Ответ верно третье уравнение 5х²+78х-4у²+8у+41=0-
3.a₁₁x²+a₂₂y²+a₃₃z²+2a₁₂xy+2a₁₃xz+2a₂₃yz+2a₁x+2a₂y+2a₃z+a₀=0, - общее уравнение поверхности второго порядка. В вашем случае
a₁₁=2,a₂₂=8,a₃₃=−7,a₁₂=0,a₁₃=0,a₂₃=0,a₁=−4,a₂=8,a₃=28,a₀=−40.
Вычислим ортогональные инварианты τ₁, τ₂, δ, Δ.
τ₁=a₁₁+a₂₂+a₃₃=2+8+(−7)=3
τ₂=(2*8-0*0)+(2*(-7)-0*0)+(8*(-7)-0*0)= -54<0;
δ=
2 0 0
0 8 0
0 0 -7=
-112≠0
Δ=
2 0 0 -4
0 8 0 8
0 0 -7 28
-4 8 28 -40=
2 0 0 -4
0 8 0 8
0 0 -7 28
0 8 28 -48=
2 0 0 -4
0 8 0 8
0 0 -7 28
0 0 28 -56=
2 0 0 -4
0 8 0 8
0 0 -7 28
0 0 0 56= 2·8·(-7)·56 = -6272<0
тип поверхности - двуполостной гиперболоид, так как δ≠0,τ₂<0;
и Δ<0
Ответ верный четвертый -двуполостной гиперболоид