Question

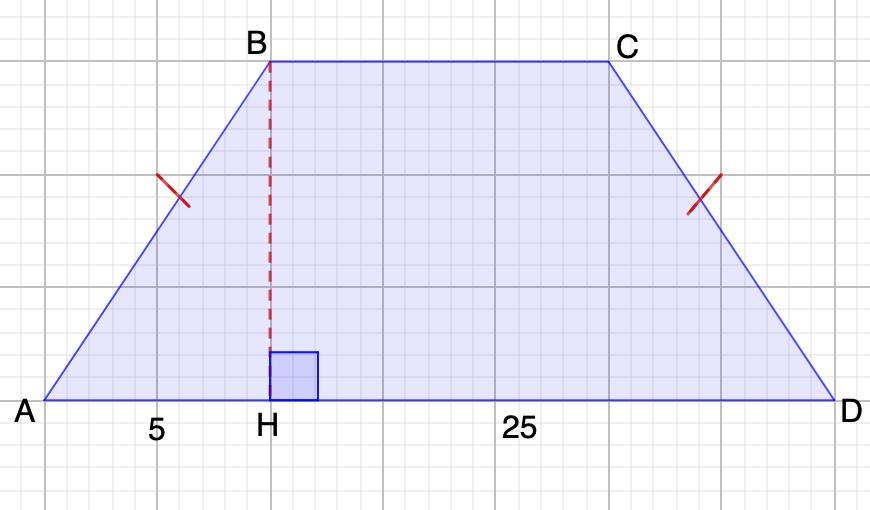
1 Высота равнобедренной трапеции, проведенная из вершины B, делит основание AD на отрезки длиной 5 и 25. Найди длину основания BC
2.Определи длину меньшего основания равнобедренной трапеции ABCD, если боковая сторона равна 10 см, угол между боковой стороной и высотой равен 30, а большее основание равно 17 см.

Answer 1

Объяснение:

Для решения этих задач воспользуемся свойством равнобедренной трапеции:

• Высота, опущенная из вершины тупого угла на большее основание, делит большее основание на части, меньшая из которых равна полуразности оснований, а большее - полусумме оснований.

1. Дано: АВСD - равнобедренная трапеция.

ВН = 5; НD = 25

Найти: ВС

Решение:

По свойству равнобедренной трапеции:

$\displaystyle AH=\frac{AD-BC}{2} \\\\5=\frac{5+25-BC}{2} \\\\10=30-BC\\\\BC=20$

2. Дано: ABCD - равнобедренная трапеция.

АВ = 10;

ВН - высота;

∠АВН = 30°;

AD = 17 см.

Найти: ВС

Решение:

Рассмотрим ΔАВН - прямоугольный.

∠АВН = 30°;

Катет, лежащий против угла 30° равен половине гипотенузы.

⇒ АН = 10 : 2 = 5

По свойству равнобедренной трапеции:

$\displaystyle AH = \frac{AD-BC}{2}\\\\5=\frac{17-BC}{2}\\\\10=17-BC\\\\BC = 7$