Предмет: Алгебра,
автор: vtoroyakkaynt41
Помогите пожалуйста срочно нужно
Приложения:
Ответы
Автор ответа:
1
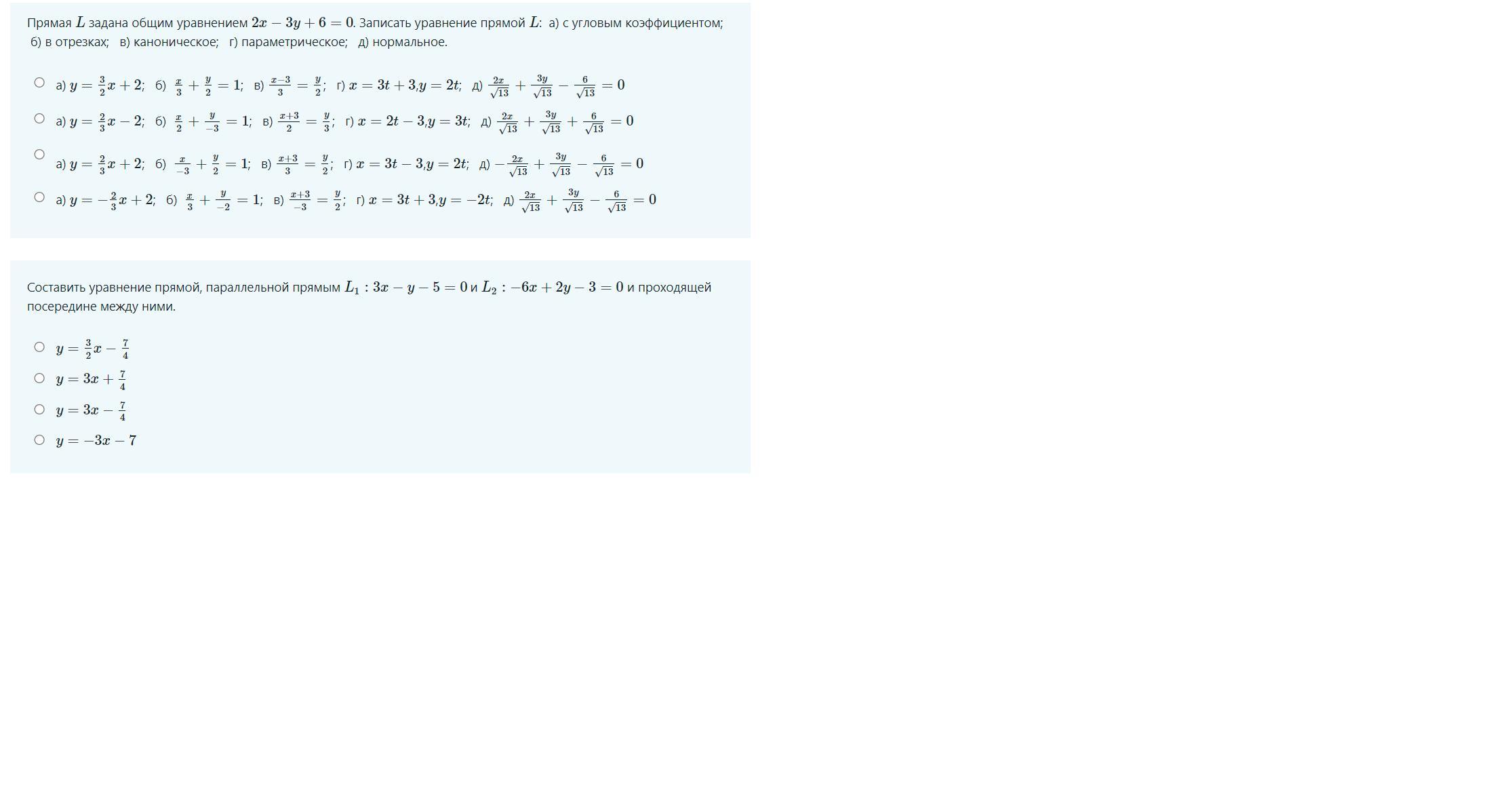
Ответ:
б) уравнение в отрезках
в) каноническое уравнение
так как
точка на прямой М(-3;0)
каноническое уравнение:
г) параметрическое:
д) нормальное:
Знак нормирующего множителя выбираем противоположным знаку свободного члена в уравнении 2х-3у+6=0 .
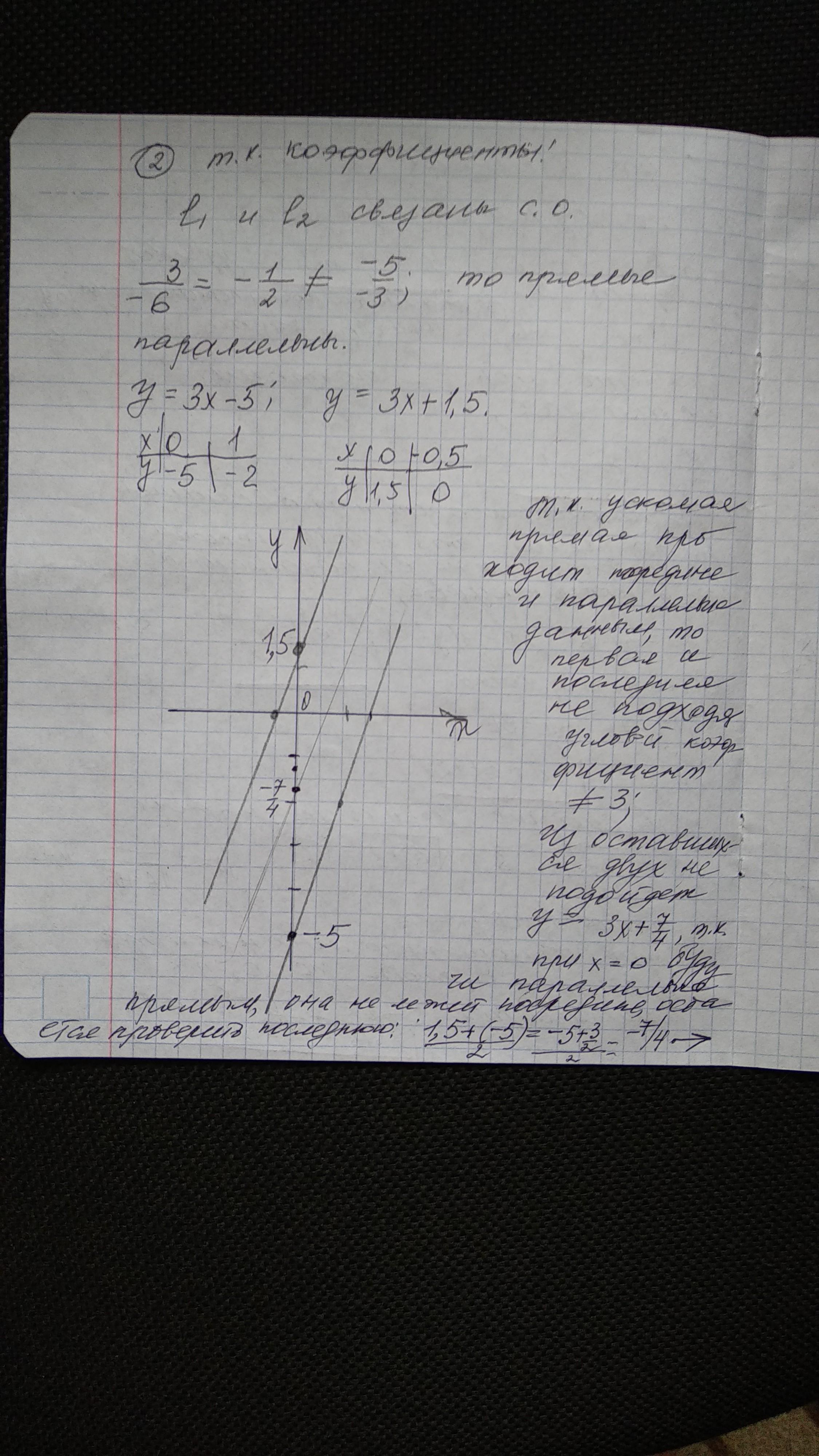
Угловые коэффициенты равны, значит прямые параллельны .
Точки пересечения прямых с осью ОУ: .
Между этими точками расстояние равно .
Значит точка, лежащая посередине между точками М₁ и М₂ , имеет ординату, равную . Тогда уравнение искомой прямой будет иметь вид:
или
.
Смотри рисунок .
Приложения:

eugeniodepez:
Здравствуйте,помогите решить задание по алгебре вопрос уже есть в профиле,буду рад если поможете)
Автор ответа:
0
Ответ: см. во вложении
Объяснение: детальное во вложении
Приложения:


Похожие вопросы
Предмет: Русский язык,
автор: danil225577
Предмет: Другие предметы,
автор: Forrtyna
Предмет: Русский язык,
автор: Артём1641186
Предмет: География,
автор: tsekvavadavid
Предмет: Русский язык,
автор: alanka2