Предмет: Математика,
автор: zzz7322
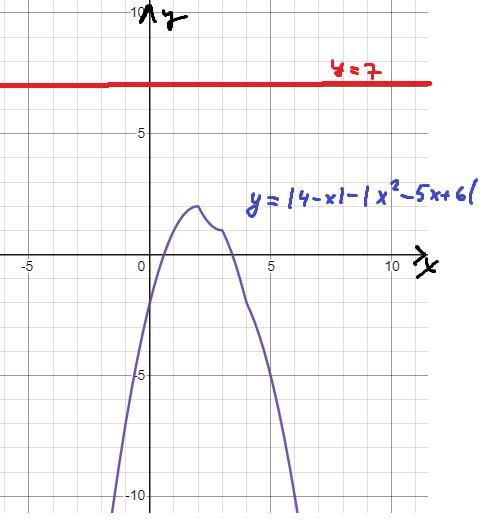
Решить уравнение
|4-х|-|х^2-5х+6|=7
Ответы
Автор ответа:
0
Ответ:
нет корней
Пошаговое объяснение:
Приложения:

zzz7322:
Здравствуйте а на оси какие числа отмечены на первой
2 и 3
Автор ответа:
0
Ответ:
(см. объяснение)
Пошаговое объяснение:
Рассмотрим неравенство:
Оно верно для любых a и b.
Пусть и
.
Тогда:
Из условия следует, что левая часть неравенства равна 7.
Значит получим:
При всех таких иксах все модули исходного уравнения раскрываются однозначно и оно принимает вид:
Это уравнение не имеет корней, а значит и исходное уравнение корней не имеет.
Уравнение решено!
Похожие вопросы
Предмет: Русский язык,
автор: Фая1111
Предмет: Українська мова,
автор: lemon46
Предмет: Русский язык,
автор: shuhratik1580
Предмет: Геометрия,
автор: БотХарви
Предмет: Алгебра,
автор: wwwdimkavolod