ПОМОГИТЕ СРОЧНО!!!?!!!

Ответы
а) Надо представить, что через сторону АВ проходит плоскость, параллельная грани SCD.
В параллельных плоскостях линии сечения плоскостью альфа параллельны.
А так как прямая АВ параллельна CD, то и линия сечения (пусть это КР) тоже параллельна CD.
Доказано – сечение ABKP пирамиды плоскостью альфа является трапецией.
б) Примем длину стороны АВ за х. Тогда по условию SA = SB = 2x.
BC = (5/4)SB = (5/4)*2x = (5/2)x.
Также из условия вытекает, что грань ASB вертикальна и высотой пирамиды является высота SE грани ASB, а треугольник ASB - равнобедренный.
Находим высоту Н = SE = √((2x)² - (x/2)²) = √(4x² - (1/4)x²) = (x/2)√15.
Площадь So основания ABCD пирамиды равна:
So = AB*BC = x*2,5x = 2,5x².
Объём пирамиды V = (1/3)SoH = (1/3)* ((5/2)x²)*((x/2)√15) = 5x³√15/12.
Приравняем заданному значению V = 30√5.
5x³√15/12 = 30√5.
Так как √15 = √3*√5, то после сокращения получим:
x³ = 6*12√5/(√3*√5) = 72/√3 = 24√3.
Отсюда находим длину стороны АВ: х = ³√(24√3) =³√(2³*3√3) = 2√3.
Тогда высота Н = SE = (x/2)√15 = (2√3/2)*√15 = √45 = 3√5.
Сторона ВС = 2,5АВ = (5/2)*2√3 = 5√3.
Теперь переходим к высоте из точки S к плоскости альфа.
Для этого через высоту пирамиды SЕ проводим секущую плоскость перпендикулярно рёбрам АВ и CD.
Грань SCD пересечётся по линии ST, а трапеция ABKP – в точке М.
ET = BC = 5√3.
ST = √(SE² + ET²) = √((45 + 75) = √120 = 2√30.
Отрезок МТ = (1/4)ST = (1/4)*( 2√30) = √30/2.
Находим по теореме косинусов EM = √(ET² + MT² - 2*ET*MT*cos(STE)) =
= √(75+(30/4)-2*(5√3)*(√30/2)*(5√3/(2√30))) = √((165/2) – (75/2)) = √45 = 3√5.
В треугольнике SET, перпендикулярном к плоскости альфа, сторона
SM = (3/4)ST = (3/4)*(2√30) = (3/2) √30.
Все стороны его найдены, определяем площадь по формуле Герона.
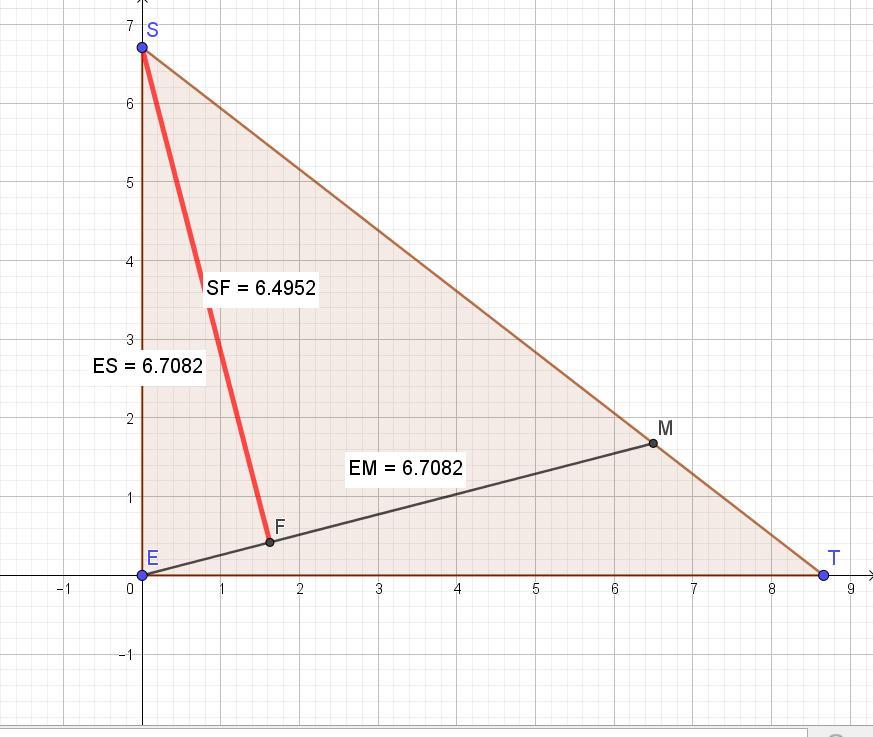
SE = EM = SM =
6,708203932 6,708203932 8,215838363
Периметр Р = 21,63224623.
Полупериметр р = 10,81612311.
S = √474,609375 ≈ 21,78553.
Высота к плоскости альфа - это высота SF к стороне ЕМ. Её находим по формуле h = 2S/EM = 2*21,78553/6,708203932 ≈ 6,4952.