Question

Даю 50 баллов, за решение задачи по геометрии!

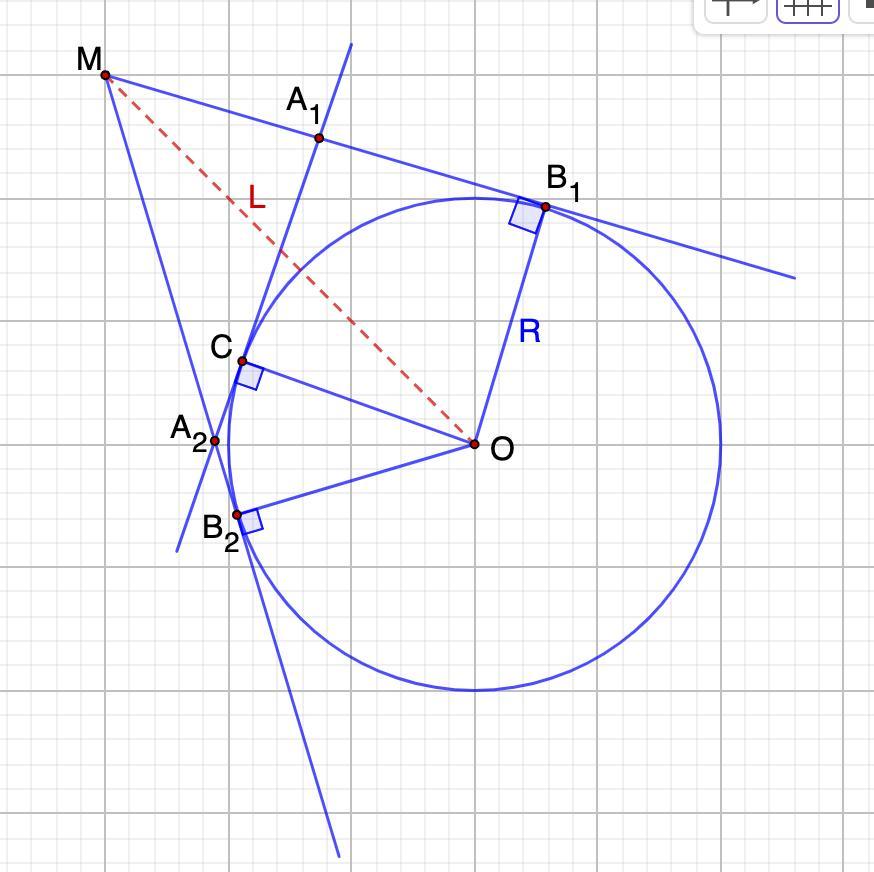
К окружности радиусом R из точки M, находящейся на расстоянии L от её центра, проведены касательные MB1 и MB2. Через произвольную точку С меньшей из дуг B1B2 проведена касательная к окружности, пересекающая отрезки MB1 и MB2 в точках A1 и A2 соответственно. Найдите периметр треугольника A1MA2.

Answer 1

Объяснение:

Дано: Окр.О,R;

MO = L

MB₁, MB₂, A₂A₁ - касательные.

Найти: Р (ΔА₁МА₂)

Решение:

1. Рассмотрим ΔОМВ₁.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОВ₁ ⊥ МВ₁ ⇒ ΔОМВ₁ - прямоугольный.

По теореме Пифагора найдем МВ₁ :

$MB_1 =\sqrt{OM^2-OB_1^2}=\sqrt{L^2-R^2}$

• 2. Отрезки касательных к окружности, проведённые из одной точки, равны.

⇒ МВ₁ = МВ₂ = $\sqrt{L^2-R^2}$

3. Рассмотрим ΔА₁МА₂

Р (ΔА₁МА₂) = А₂М + МА₁ + А₁А₂

А₁А₂ = А₁С + СА₂

А₂С = А₂В₂ ;  СА₁ = А₁В₁ (отрезки касательных)

Тогда:

Р (ΔА₁МА₂) = А₂М + МА₁ + А₁С + СА₂ = А₂М + МА₁ + А₁В₁ + А₂В₂

А₂М + А₂В₂ = МВ₂

МА₁ + А₁В₁ = МВ₁

⇒ Р (ΔА₁МА₂)  = МВ₂ + МВ₁ = $2\sqrt{L^2-R^2}$