Предмет: Геометрия,
автор: tatanasajnahova04
В прямоугольный треугольник ABC с прямым углом
ABC вписан прямоугольный треугольник СКВ.
Катеты треугольника АВС имеют размер 45 и 60 см.
Отрезок KA на 21 см больше отрезка СК. Найдите
Отношение площадей двух треугольников. Ответ
Округлите до десятых.
Приложения:
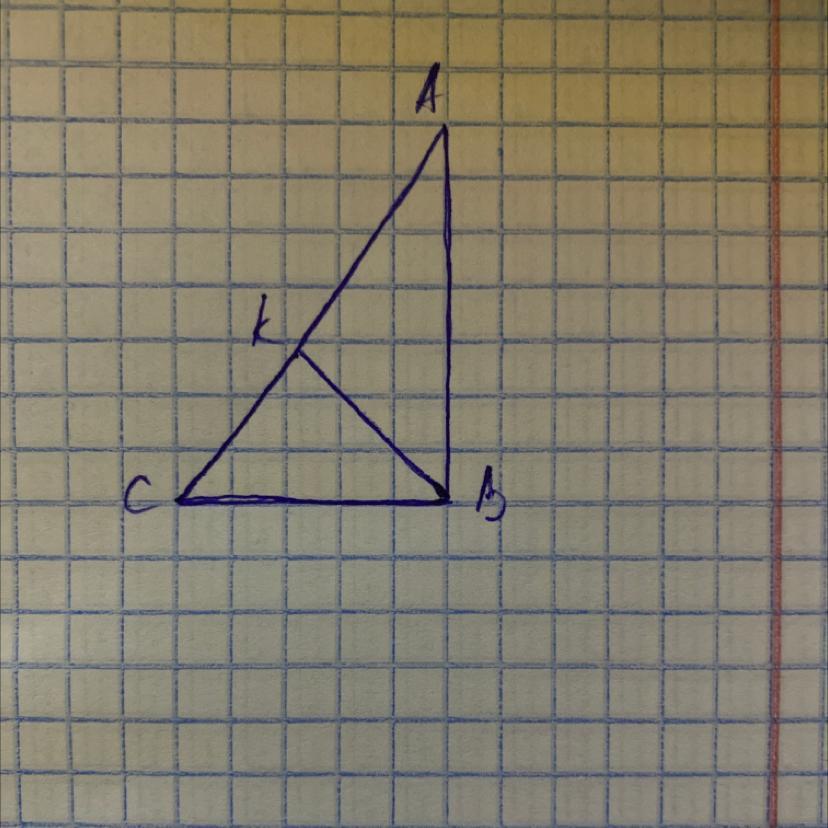
Ответы
Автор ответа:
5
Ответ:
Так как вписан прямоугольный треугольник CKB угол CKB — прямой, а следовательно и угол AKB тоже прямой, так как они смежные.
CB=45 и AB=60 — катеты, AC — гипотенуза
По теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы.
CK+KA=75
KA=CK+21
CK+(CK+21)=75
2CK=75-21
2CK=54
CK=27
KA=27+21=48
Найдем длину BK по той же теореме Пифагора:
CB²=CK²+BK²
BK²=CB²-CK²
Найдем площадь треугольника AKB по формуле S=(ab)/2, где a и b катеты
Теперь найдем площадь треугольника CKB:
Отношение площадей треугольников AKB и CKB
S(ΔAKB):S(ΔCKB) = 16:9
Похожие вопросы
Предмет: Русский язык,
автор: Тиктоничка
Предмет: Русский язык,
автор: kristina0110
Предмет: Українська мова,
автор: alexfuerte07
Предмет: Математика,
автор: zgonnikovakisa11
Предмет: Алгебра,
автор: imasuk850