6. Більша основа рівнобічної трапеції дорівнює 42 см, бічна сторона 18 см, а кут між ними - 60°. Знайди середню лінію трапеції.
Ответы
Ответ:
33 см.
Объяснение:
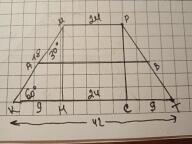
Дано: КМРТ - трапеція, КМ=РТ=18 см, КТ=42 см, ∠К=∠Т=60°, АВ - середня лінія. АВ - ?
Проведемо висоти МН та РС. ΔКМН=ΔТРС за двома кутами, тому КН=СТ.
ΔКМН - прямокутний,
∠К=60°, отже ∠КМН=30°, а КН=1/2 КМ = 18:2=9 см.
СТ=КН=9 см; МР=СН=42-9-9=24 см.
Середня лінія трапеції дорівнює напівсумі основ.
АВ=(МР+КТ):2=(24+42):2=33 см
Ответ:33 см
Объяснение:
опустим на нижнее большее основание две высоты из вершин тупых лов, отрезки, начиная от нижних вершин бок. сторон равны по 9 см, т.к. лежат в прямоугольных треугольниках, составленных из высот бок. сторон и отсекаемых высотами отрезков нижнего основания, значит, верхнее основание равно 42-2*9=42-1824/см/, и тогда средняя линия равна полусумме оснований. т.е. (42+24)/2=66/2=33/см/