Question

помогите решить 3 вот этих номера, пожалуйста- 100 баллов

Answer 1

Объяснение:

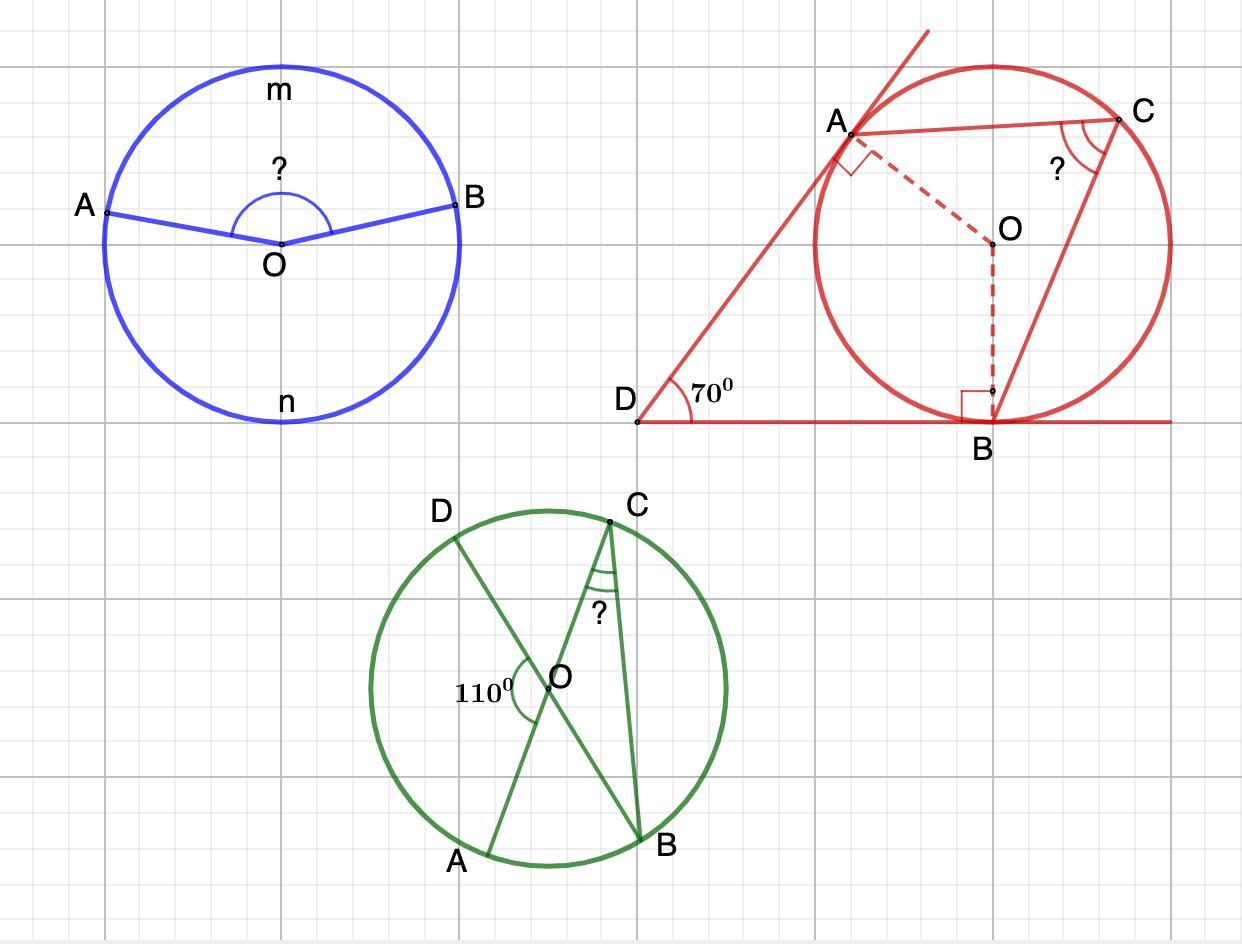
8.

Дано: Окр.О;

∪AmB : ∪AnB = 9 : 11

Найти: ∠АОВ

Решение:

Вся окружность - 360°.

Пусть ∪AmB = 9x, тогда ∪AnB = 11x.

Составим уравнение:

9х + 11х = 360°

20х = 360°

х = 18°

⇒ ∪АmB = 18°·9 = 162°

• Центральный угол равен градусной мере дуги, на которую он опирается.

⇒ ∠АОВ = 162° (центральный).

9.

Дано: ∠D = 70°

Окр.О - вписанная;

Найти: ∠АСВ

Решение:

Рассмотрим DACB.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ∠DAO = ∠OBD = 90°

• Сумма углов четырехугольника равна 360°.

⇒ ∠АОВ = 360° - ( 70° + 90° + 90°) = 110°

• Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

⇒ ∠АСВ = ∠АОВ : 2 = 110° : 2 = 55° (вписанный)

10.

Дано: Окр.О

АС и ВD - диаметры.

∠AOD = 110° - центральный.

Найти: ∠АСВ

Решение:

• Центральный угол равен градусной мере дуги, на которую он опирается.

⇒ ∪AD = ∠AOD = 110°

• Диаметр делит окружность на две полуокружности.

⇒ ∪DAB = 180°

∪AB = 180° - ∪AD = 180° - 110° = 70°

• Вписанный угол равен половине градусной меры дуги, на которую он опирается.

⇒ ∠ACB = ∪AB : 2 = 70° : 2 = 35°