Подскажите как решать, пожалуйста!
Спасибо!
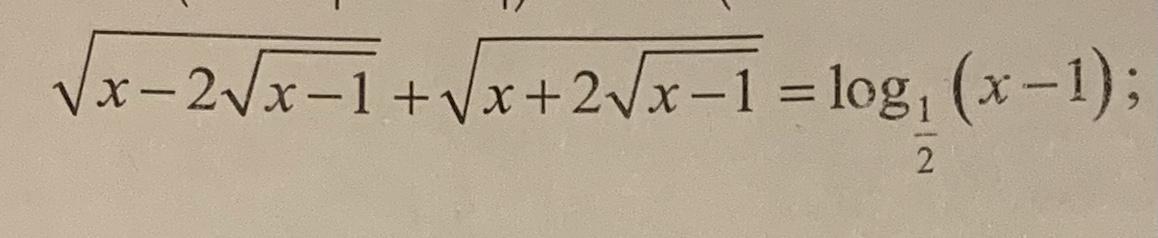
Ответы
Ответ:
(см. объяснение)
Объяснение:
(при решении для удобства будем делать замены)
Пусть и
⇒
: корней нет (очевидно).
: (⇒
):
Подставляем :
Замечаем, что .
Причем, так как у нас , модуль раскрывается однозначно:
⇒
Вернемся от к иксам:
То есть уравнение свелось к виду:
У нас выше показано, что .
Значит будет только:
Решая это уравнение получаем, что .
Уравнение решено!
Ответ:
x=5/4=1.25
Объяснение:
Корень квадратный сам по себе неотрицателен (√4=2, √9=3 и т.д.), то есть √х≥0 и сумма корней тоже величина неотрицательна.
Так как левая часть уравнения у нас неотрицательна, то и правая часть должна быть неотрицательной. Поэтому, прежде чем решать уравнение, сделаем ограничение на правую часть (надо чтобы она была неотрицательной)
Таким образом, все корни мы будем искать в этом промежутке
Решение:
Мы выяснили, что обе части неравенства неотрицательны, значит мы можем их возвести в квадрат:
Мы рассматриваем только 1<x≤2, и при подстановки любого икса из этого промежутка под модулем получается отрицательное число, значит этот модуль мы раскрываем с противоположным знаком, то есть |x-2|=-(x-2)=-x+2=2-x
x=5 - не подходит под наш промежуток (1;2], значит корень только x=5/4
Конечно, при решении мы еще не учли ОДЗ квадратных корней, поэтому остается просто подставить x=5/4 в исходное уравнение и убедится, что он нам подходит
Проверка:
Проверка пройдена!