Question

Срочно помогите решить задачу

Answer 1

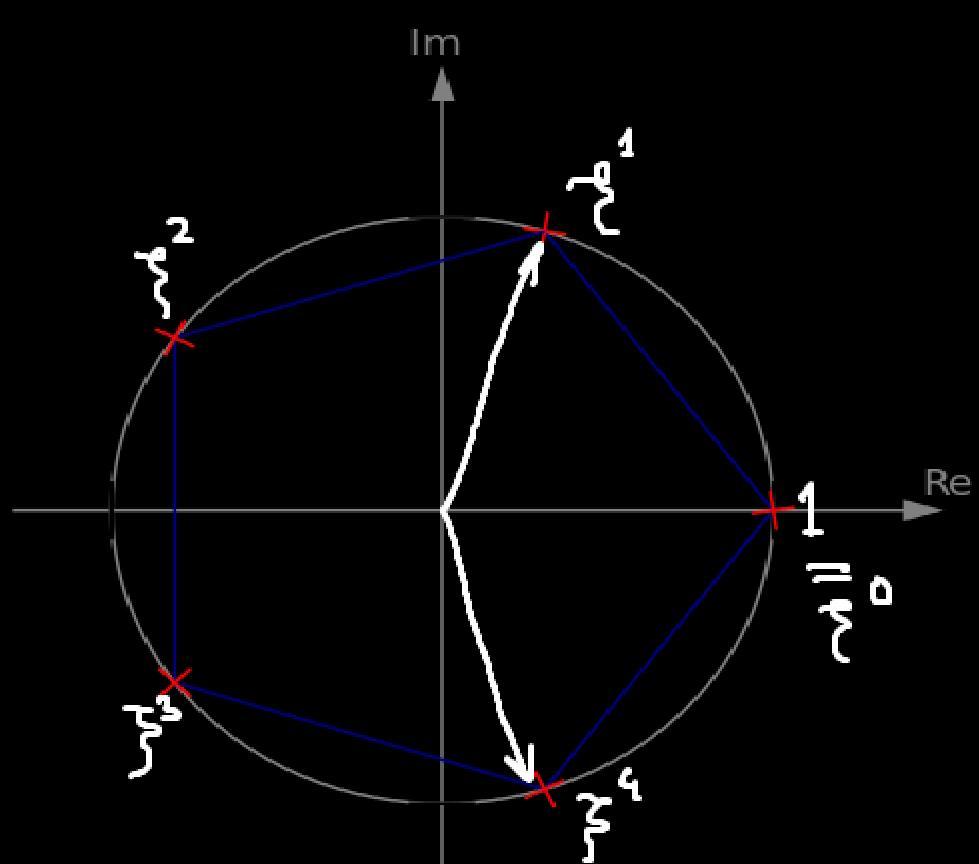
Здесь существует достаточно простая интерпретация: правильный $n$-угольник -- это по сути множество $\zeta^{j},\; j=\overline{0,n-1}$, где $\zeta$ -- корень $n$-ой степени из единицы.

Прежде чем рассматривать случай произвольного $n$, рассмотрим случай пятиугольника. Заметим, что у него один вид стороны (как и у любого правильного многоугольника) и один вид диагонали (коих в нем $5$). Тогда  требуется посчитать сумму $\underbrace{5|\zeta^0-\zeta^1|^2}_{\text{sum of sides' squares}} + \underbrace{5|\zeta^2-\zeta^4|^2}_{\text{sum of diagonals' squares}}$.

Ее же можно переписать и иначе: $5\left(\left(1-\cos\dfrac{2\pi}{5}\right)^2+\sin^2\dfrac{2\pi}{5}+\left(\cos\dfrac{4\pi}{5}-\cos \dfrac{8\pi}{5}\right)^2+\left(\sin\dfrac{4\pi}{5}-\sin\dfrac{8\pi}{5}\right)^2\right)$, раскрыть это не очень страшно, поскольку многие синусы и косинусы сольются в единицу: $5\left(4-2\left(\cos\dfrac{2\pi}{5}+\cos\dfrac{4\pi}{5}\right)\right)$. Теперь отметим, что $\cos \dfrac{\pi}{5}+\cos \dfrac{2\pi}{5}+\cos \dfrac{3\pi}{5}+\cos \dfrac{4\pi}{5} = 0$ и $\cos \dfrac{2\pi}{5}+\cos \dfrac{4\pi}{5}=\cos \dfrac{\pi}{5}+\cos \dfrac{3\pi}{5}$ -- все это следует из картинки и симметрии (первое -- из суммы всех степеней корня пятой степени из единицы). Но тогда искомая сумма равна $-1/2$, а ответ -- $25 = 5^2$. То, что искомая величина оказалась равной квадрату числа сторон -- не случайность.

Теперь считаем в общем виде:

$\dfrac{n}{2}\left(|\zeta^{0}-\zeta^1|^2 +|\zeta^0-\zeta^2|^2+|\zeta^0-\zeta^3|^2+\ldots+|\zeta^0-\zeta^{n-1}|^2\right)$. Переписывая в тригонометрической форме: $\dfrac{n}{2}\left(\sum\limits_{j=1}^{n-1}\left[\left(1-\cos\dfrac{2\pi j}{n}\right)^2+\sin^2\dfrac{2\pi j}{n}\right]\right) = \dfrac{n}{2}\left(n-1-2\sum\limits_{j=1}^{n-1}\cos\dfrac{2\pi j}{n}+n-1\right)$. Осталось заметить, что $\sum\limits_{j=0}^{n-1}\cos\dfrac{2\pi j}{n}$ есть сумма действительных частей всех корней, а потому равна нулю (поскольку вся сумма равна нулю), значит, $\sum\limits_{j=1}^{n-1}\cos \dfrac{2\pi j}{n} = -1$, следовательно, искомая сумма равна $\dfrac{n}{2}(n-1+2+n-1) = n^2$.