Предмет: Алгебра,
автор: oksan4ik4
Найдите наибольшее и наименьшее значение функции f(x)=x^3−12x^2+36x+5 на промежутке [1; 4]
Ответы
Автор ответа:
1
Объяснение:
также пишу алгоритм нахождения:
1. Найти ОДЗ если нужно
2. Найти производную
3. Приравнять производную к 0 и найти критические точки
4. Выяснить какие из этих точек принадлежат промежутку
5. Вычислить значение функции в критических точках и на концах отрезка
6. Из полученных значений выбрать наибольшее и наименьшее
Приложения:

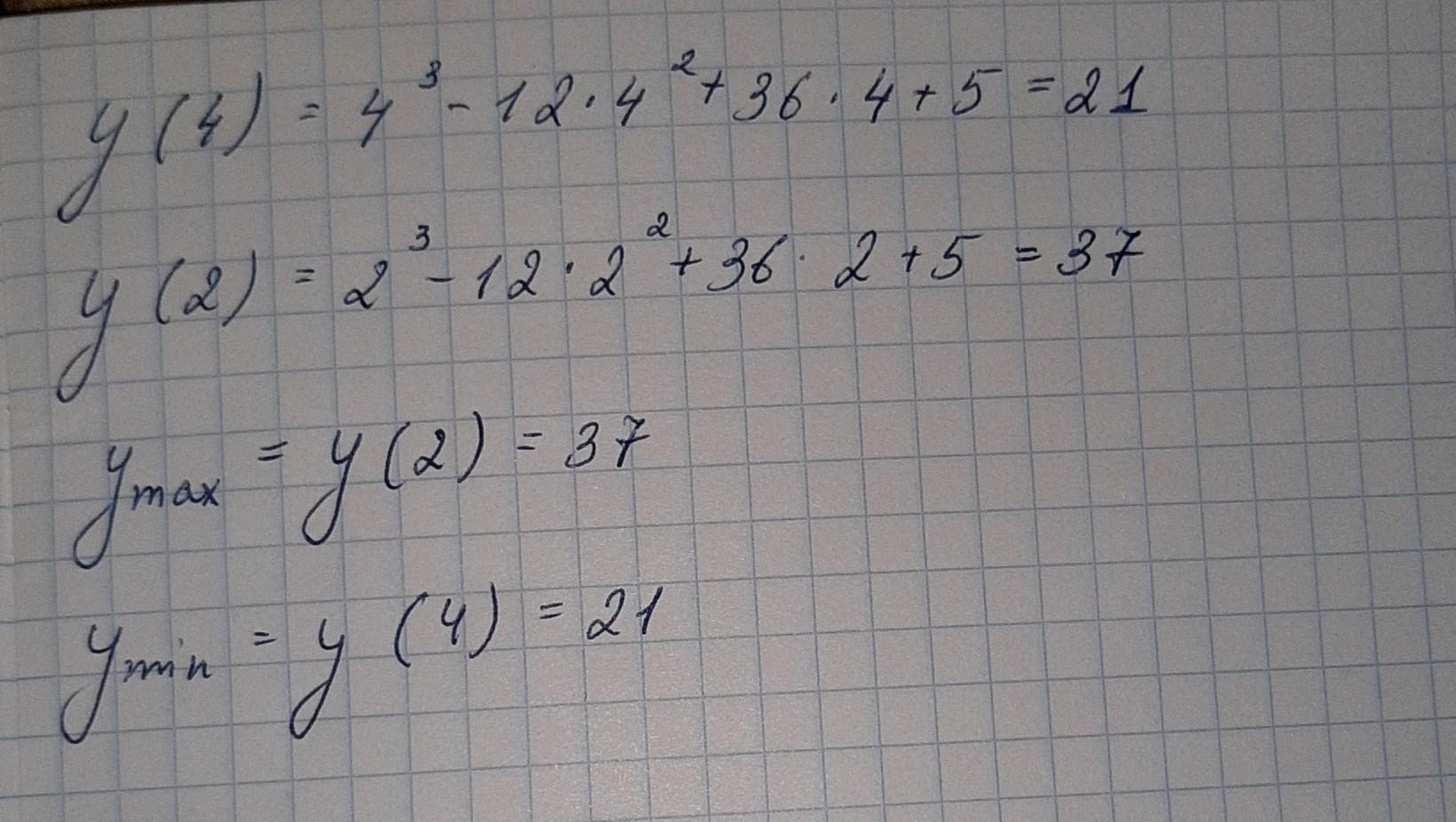
Автор ответа:
1
Объяснение:
Найдем значение функции на концах промежутка:
Найдем экстремумы функции.
Найдем производную:
Приравняем к 0 и найдем корни:
Отметим точки на числовой оси и определим знаки производной на промежутках:
К данному промежутку точка х=6 не относится.
В точке х=2 производная меняет знак с "+" на "-". Следовательно в данной точке - max.
Найдем значение функции при х=2:
Имеем:
f(x) наиб. = f(2) = 37
f(x) наим. = f(4) = 21
Похожие вопросы
Предмет: Английский язык,
автор: arman52
Предмет: Українська мова,
автор: Георгий1709
Предмет: Русский язык,
автор: мирослав10
Предмет: Английский язык,
автор: bassbooster77
Предмет: Математика,
автор: deliurek96