Предмет: Математика,
автор: zuzuaa
Даю 50 баллов!!
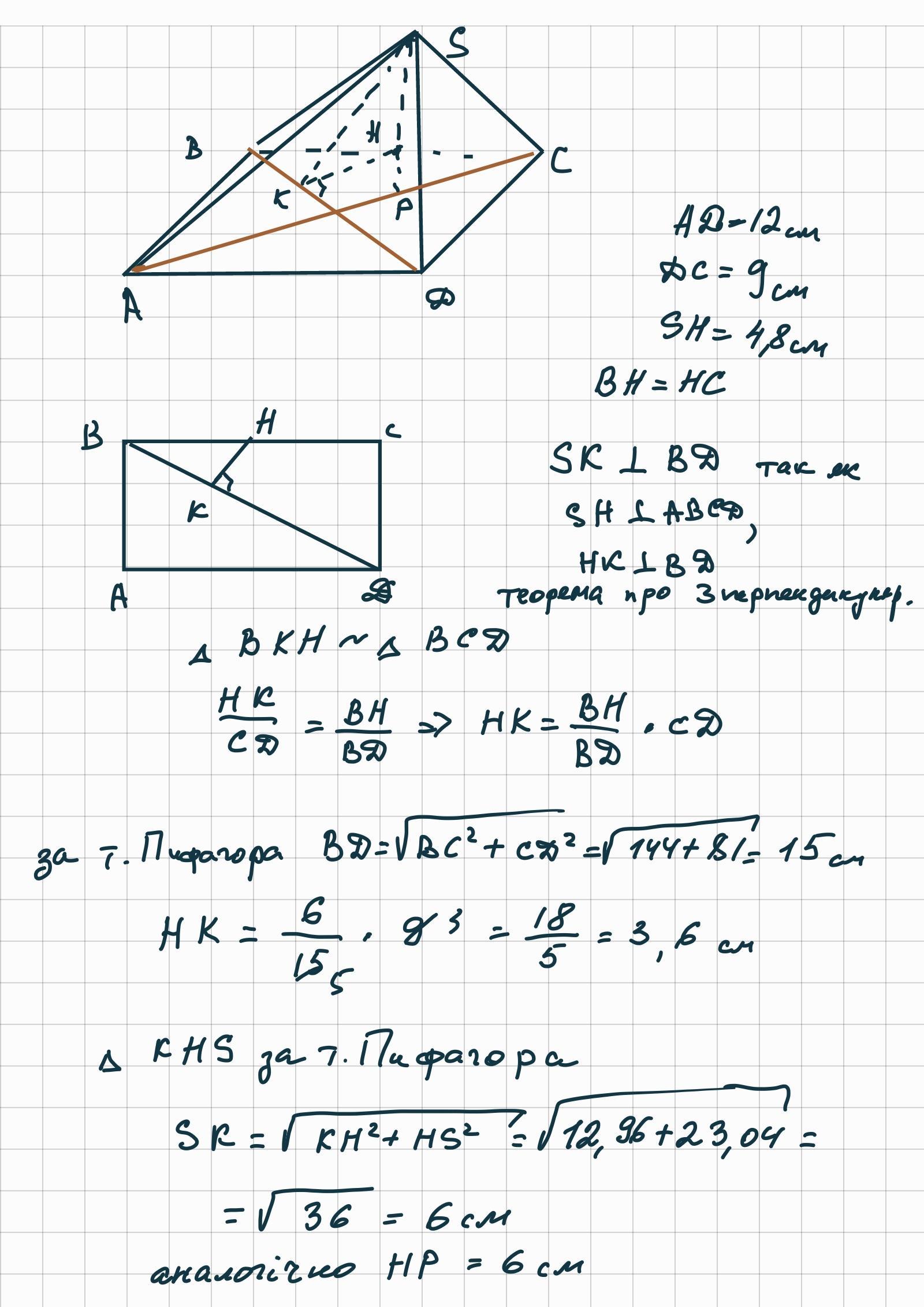
Сторони прямокутника дорівнюють 9 см і 12 см. Із середини більшої сторони прямокутника проведено перпендикуляр до його площини довжиною 4,8 см. Знайдіть відстань від кінця цього перпендикуляра до діагоналей прямокутника.
Ответы
Автор ответа:
0
Відповідь:
Покрокове пояснення:
Приложения:
Автор ответа:
1
Ответ: по 6 см .
Пошаговое объяснение:
ABCD - прямокутник : АВ = 9 см , ВС = 12 см ; ВК = КС = 6 см ;
МК⊥(АВС) ; MK = 4,8 cм . МР⊥BD , MN⊥AC . Так як
ΔBKP = ΔCKN за гіпотенузою і гострим кутом , то KP = PN . А із
рівності прямок . тр - ків ΔMKP = ΔMKN ( за двома катетами )
випливає MP = MN . У прямок . ΔВDС BD = √ ( BC² + DC² ) =
= √ ( 12² + 9² ) = √ ( 144 + 81 ) = √ 225 = 15 ( см ) .
Прямок . ΔBKP∼ΔBDC за гострим ∠DBС , тоді BK/BD = KP/DC ;
KP = ( DC * BK )/BD = ( 9 * 6 )/15 = 3,6 ( см ) ; КР = 3,6 см .
Із прямок , ΔMPK : MP = √ ( 4,8² + 3,6² ) = √ 36 = 6 ( см ) .
В - дь : MP = MN = 6 cм .
Похожие вопросы
Предмет: Русский язык,
автор: дарья957
Предмет: Другие предметы,
автор: Kitty0
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: nastena2007nastya