Question

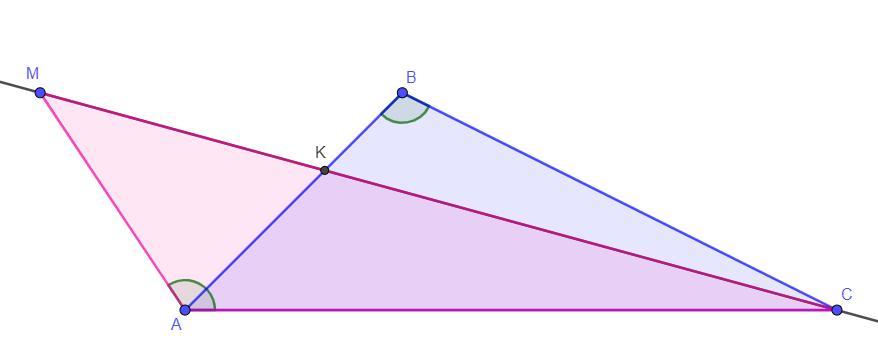
Стороны ab,bc и ac треугольника abc равны соответственно 3,корень 6 и 2корень5. Точка M расположена вне треугольника abc, причём отрезок CM пересекает сторону ab в точке отличной от B. Известно что треугольник с вершинами M,A,C подобен исходному. Найдите косинус угла MAC, если угол MAC < 90°

Answer 1

Ответ:

$\boxed{ \cos \angle MAC = - \dfrac{5\sqrt{6} }{36}}$

Объяснение:

Дано: AB = 3, $BC = \sqrt{6}$, $AC = 2\sqrt{5}$, $зMAC \sim зABC$, ∠MAC > 90°

Найти: cos ∠MAC - ?

Решение: По теореме косинусов для треугольника ΔABC:

$AB^{2} + BC^{2} - 2 \cdot AB \cdot BC \cdot \cos \angle ABC = AC^{2}$

$\angle \cos ABC = \dfrac{AB^{2} + BC^{2} - AC^{2}}{2 \cdot AB \cdot BC } = \dfrac{3^{2} + (\sqrt{6} )^{2} - (2\sqrt{5} )^{2}}{2 \cdot 3 \cdot \sqrt{6} } = \dfrac{9 + 6 - 20}{6\sqrt{6} } =$

$= \dfrac{15 - 20}{6\sqrt{6} } = -\dfrac{5}{6\sqrt{6} } = -\dfrac{5 \cdot \sqrt{6} }{6\sqrt{6} \cdot \sqrt{6} }= - \dfrac{5\sqrt{6} }{36}$.

Так как по условию треугольник $зMAC \sim зABC$, то по свойствам подобных треугольников их соответствующие углы равны. Так как в треугольнике только 1 угол может быть может быть тупым, то угол ∠ABC > 90°, так как cos ∠ABC < 0. Тогда ∠ABC = ∠MAC, следовательно cos ∠ABC = cos ∠MAC = $- \dfrac{5\sqrt{6} }{36}$.