Предмет: Алгебра,
автор: jurayevm239
Помогите решить производную
Приложения:

Ответы
Автор ответа:
2
Ответ: -3
Объяснение:
, следовательно,
Таким образом:
Подставим вместо х
Автор ответа:
0
Ответ:
Объяснение:
Решение дано на фото.
Приложения:
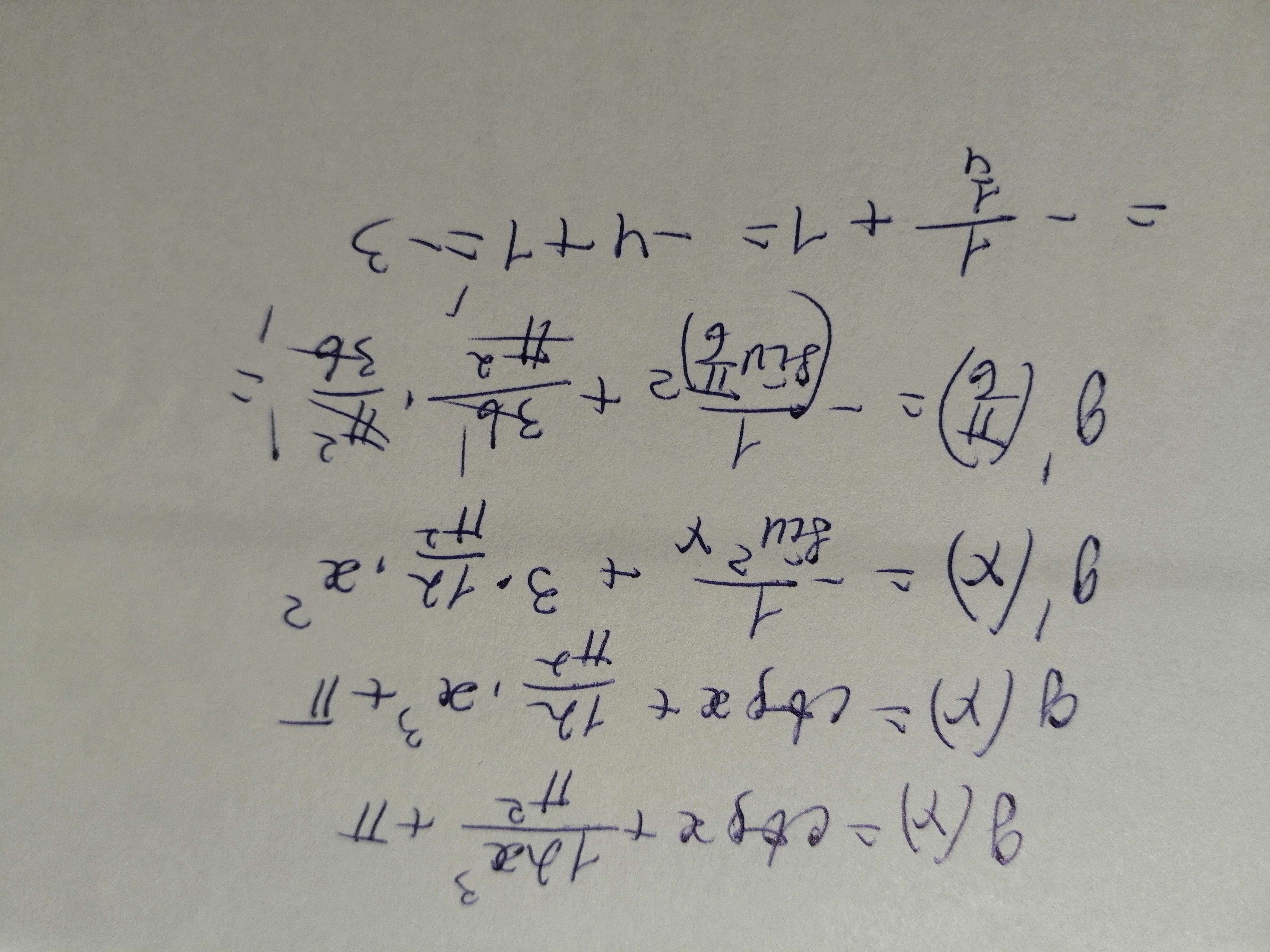
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Шарапат1
Предмет: Английский язык,
автор: AniaLoveGood
Предмет: Русский язык,
автор: Уля205
Предмет: Английский язык,
автор: kakka72
Предмет: Математика,
автор: gugu2007