Предмет: Геометрия,
автор: stas140573
Помогите,плиз геометрия восьмой класс
Приложения:
margaritakiseleva:
уже учили теорему Пифагора?
да
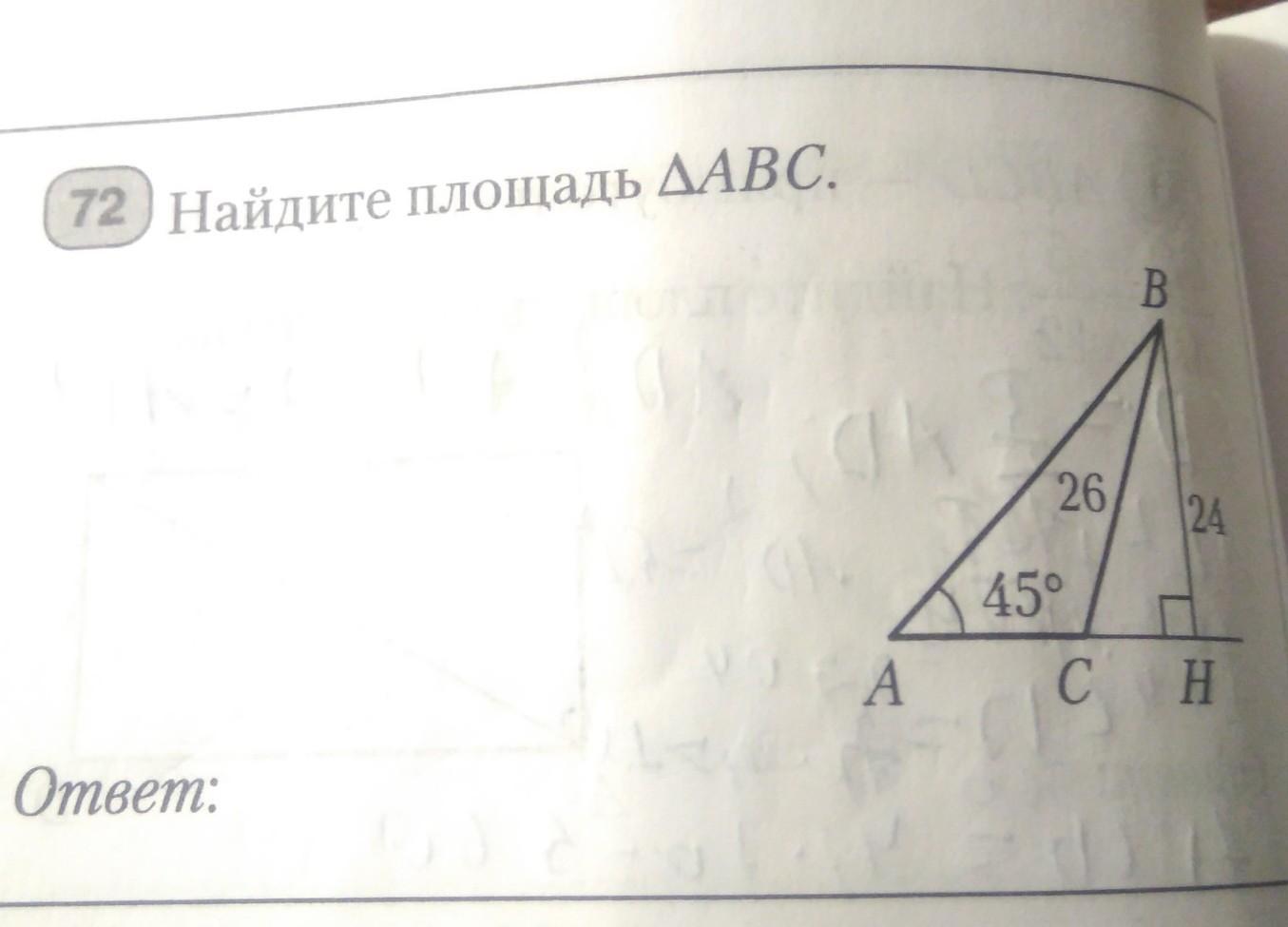
в задачи просили найти площадь не всего треугольника, а АВС
Ответы
Автор ответа:
2
Ответ:
168 кв ед
Объяснение:
1)Рассмотрим прямоугольный треугольник АВН(<Н=90°)
<В=90°-45°=45° => треугольник АВН - равнобедренный. АН=ВН=24
- Площадь прямоугольного треугольника равна половине произведения его катетов :
а=АН=24, b=ВН=24
тогда площадь треугольника АВН равна:
кв.ед.
2)Рассмотрим прямоугольный треугольник CВН(<Н=90°)
По теореме Пифагора найдём катет СН:
Площадь треугольника СВН (катет а=СН=10, катет b=ВН=24):
кв. ед.
Площадь треугольника ABC равна разности площадей треугольников АВН и СВН:
S(ABC)=S(ABH)-S(CBH)=288-120=168 кв ед.
Автор ответа:
2
Ответ:
168ед²
Объяснение:
∆ABH- прямоугольный равнобедренный треугольник.
<ВНС=90°; <ВАН=45°; <АВН=45°, углы при основании равны.
АН=ВН=24ед.
∆ВСН- прямоугольный треугольник
По теореме Пифагора
СН=√(ВС²-ВН²)=√(26²-24²)=√(676-576)=
=√100=10ед.
АС=АН-СН=24-10=14ед.
S(∆ABC)=1/2*AC*BH=1/2*14*24=168ед²
Похожие вопросы
Предмет: Русский язык,
автор: Гадыр
Предмет: Қазақ тiлi,
автор: Макс330027
Предмет: Русский язык,
автор: 222311
Предмет: Информатика,
автор: kamm1laa
Предмет: География,
автор: malanuhalilia