Question

Периметр прямокутного трикутника дорівнює 80 см, а гіпотенуза - 34 см. Знайдіть площу трикутника.
Даю 70 балів!

Answer 1

Ответ:

$\boxed{S_{зABC} = 240}$ см²

Объяснение:

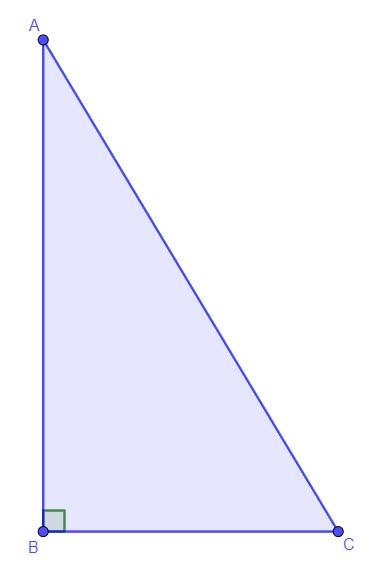
Дано: ∠ABC = 90°, AC = 34 см, PΔABC = 80 см

Знайти: $S_{зABC}$ - ?

Розв'язання: За означенням периметра трикутника (ΔABC):

PΔABC = AB + BC + AC ⇒ AB + BC = PΔABC - AC = 80 см - 34 см = 46 см. За теоремою Піфагора: $AB^{2} + BC^{2} = AC^{2} = 34^{2} = 1156$ см². За формулою площі прямокутного трикутника: $S_{зABC} = \dfrac{AB \cdot BC}{2}$.

AB + BC = 46

(AB + BC)² = 46²

AB² + BC² + 2 · AB · BC = 2116

2 · AB · BC = 2116 - (AB² + BC²)

2 · AB · BC = 2116 - AC²

2 · AB · BC = 2116 - 1156

2 · AB · BC = 960|:4

$\dfrac{AB \cdot BC}{2} = 240$

$S_{зABC} = 240$ см².